Let the disk of mass 2.5kg start from rest at time t = 0 and also let the tension in the massless cord be 6.0 N and the angular acceleration of the disk be −24rad/s2. What is its rotational kinetic energy K at t = 2.5 s?
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the given values
- Mass of the disk, m=2.5kg
- Tension in the cord, T=6.0N
- Angular acceleration, α=−24rad/s2
- Time, t=2.5s
- Initial angular velocity, ω0=0rad/s (since it starts from rest)
Step 2: Calculate the angular velocity at t=2.5s
Using the formula for angular velocity:
ω=ω0+αt
Substituting the values:
ω=0+(−24rad/s2)×(2.5s)=−60rad/s
Step 3: Calculate the moment of inertia I of the disk
The moment of inertia I for a disk is given by:
I=12mr2
Assuming the radius r=0.2m (as it is not provided in the question, we can assume a common radius for a disk):
I=12×2.5kg×(0.2m)2=12×2.5×0.04=0.05kg m2
Step 4: Calculate the rotational kinetic energy K
The rotational kinetic energy K is given by:
K=12Iω2
Substituting the values of I and ω:
K=12×0.05kg m2×(−60rad/s)2
Calculating (−60)2=3600:
K=12×0.05×3600=0.025×3600=90J
Final Answer
The rotational kinetic energy K at t=2.5s is 90J.
---
- Mass of the disk, m=2.5kg
- Tension in the cord, T=6.0N
- Angular acceleration, α=−24rad/s2
- Time, t=2.5s
- Initial angular velocity, ω0=0rad/s (since it starts from rest)
Using the formula for angular velocity:
ω=ω0+αt
Substituting the values:
ω=0+(−24rad/s2)×(2.5s)=−60rad/s
The moment of inertia I for a disk is given by:
I=12mr2
Assuming the radius r=0.2m (as it is not provided in the question, we can assume a common radius for a disk):
I=12×2.5kg×(0.2m)2=12×2.5×0.04=0.05kg m2
The rotational kinetic energy K is given by:
K=12Iω2
Substituting the values of I and ω:
K=12×0.05kg m2×(−60rad/s)2
Calculating (−60)2=3600:
K=12×0.05×3600=0.025×3600=90J
The rotational kinetic energy K at t=2.5s is 90J.
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
(a) A uniform 2.00 kg disk of radius 0.300 m can rotate around its central axis like a merry-go-round. Beginning from rest at time t = 0, it undergoes a constant angular acceleration of 30.0rad/s2. When is the rotational kinetic energy equal to 2000 J? (b) Repeat the calculation but substitute a ring of the same mass and radius and assume that the spokes have negligible mass.
View SolutionA wheel starting from rest via rotating with a constant angular velocity of 3 rad s−1. What is its angular acceleration after 4 s?
View Solution
Knowledge Check
the angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
A10rads2B5rads2CZeroD3rads2A samll object of mass 10.0 g is at rest 30.0 cm from a horizontal disk's centre. The disk starts to rotate from rest about its centre with a constant angular acceleration of 4.50 rad/s2. What is the magnitude of the net force acting on the object after a time of t=13 s if the object remains at rest with respect to the disk ?
A0NB1.5×10−2NC7.4×10−3ND1.8×10−2NStarting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
AAt t=2s, the position of the particle is at x=9mBParticle acceleration at t=2s is 1m/s2CParticle acceleration is 1/2m/s2 through out the motionDParticle will never go in negative direction from it's starting position
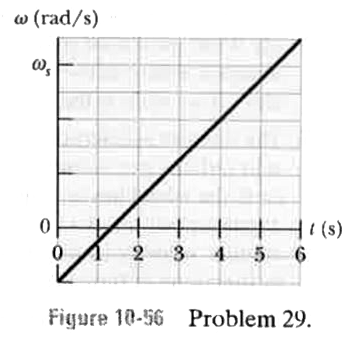
Figure 10-56 gives angular speed versus time for a thin rod that rotates around one end. The scale on the ω axis is set by ωs=60rad/s. (a) What is the magnitude of the rod's angular acceleration? (b) At t = 4.0 s, the rod has a rotational kinetic energy of 1.60 J. What is its kinetic energy at t = 0?
View SolutionFigure shows a uniform disk, with mass M = 2.5 kg and radius R = 20 cm, mounted on a fixed horizontal axle. A block with mass m = 1.2 kg hangs from a massless cord that is wrapped around the rim of the disk. Find the acceleration of the falling block, the angular acceleration of the disk, and the tension in the cord. The cord does not slip, and there is no friction at the axle.
View SolutionA constant torque is acting on a wheel. If starting from rest, the wheel makes n rotations in t seconds, show that the angular
acceleration is given by α=4πnt2rads−2.
View SolutionA disc, initially at rest, starts rotating about its own axis/ with a constant angular acceleration of 0*2 rad/s2. The time taken by the disc to rotate by 10 rad (in seconds) is
View SolutionA disc of radius 0.1 m starts from rest with an angular acceleration of 4.4rad/s2 .Then linear velocity of the point on its after 5 s is
View Solution
