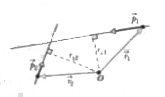
Figure shows an overhead view of two particles moving at constant momentum along horizontal paths.
Particle 1, with momentum magnitude $p_{1} = 5.0 k g \cdot m / s$ , has position vector ${\to r}_{1}$ and will pass 2.0 m from point O.
Particle 2, with momentum magnitude $p_{2} = 2.0 k g \cdot m / s$ , has position vector ${\to r}_{2}$ and will pass 4.0 m from point O. What are the magnitude and direction of the net angular momentum $\to L$ about point O of the two particle system?

Text Solution

Verified by Experts

To find $\to L$ , we can first find the individual angular momenta ${\to l}_{1} and {\to l}_{2}$ and then add them. To evaluate their magnitudes, we can use any one of Eqs. Through. However, Eq. is easiest, because we are given the perpendicular distances $r_{⊥ 1} (= 2.0 m) and r_{⊥ 2} (= 4.0 m)$ and the momentum magnitudes $p_{1} and p_{2}$ .
Calculations: For particle 1, Eq. yields
$l_{1} = r_{⊥ 1} p_{1} = (2.0) (5.0 k g \cdot m / s)$
= $10 k g \cdot m^{2} / s$ .
To find the direction of vector ${\to l}_{1}$ , we use Eq. and the right-hand rule for vector products. For ${\to r}_{1} \times {\to p}_{1}$ , the vector product is out of the page, perpendicular to the plane of Fig. This is the positive direction, consistent with the counterclockwise rotation of the particle.s position vector ${\to r}_{1}$ around O as particle 1 moves. Thus, the angular momentum vector for particle 1 is
$l_{1} = + 10 k g \cdot m^{2} / s$ .

Similarly, the magnitude of ${\to l}_{2}$ is
$l = r_{⊥ 2} p_{2} = (4.0 m) (2.0 k g \cdot m / s)$
= $8.0 k g \cdot m^{2} / s$ ,
and the vector product ${\to r}_{2} \times {\to p}_{2}$ is into the page, which is the negative direction, consistent with the clockwise rotation momentum vector for particle 2 is
$l_{2} = - 8.0 k g \cdot m^{2} / s$
The net angular momentum for the two particle system is
$L = l_{1} + l_{2} = + 10 k g \cdot m^{2} / s + (- 8.0 k g \cdot m^{2} / s)$
= $+ 2.0 k g \cdot m^{2} / s$ .

Updated on:21/07/2023

The position vector $\to r$ and linear momentum $\to p$ and $\to r = ˆ i$ and $\to p = 4 ˆ j$ the angular momentum vector is perpendicular to
Ax-axis
By-axis
Cz-axis
Dxy-plane
A particle is projected at time t=0 from a point P on the ground with a speed $v_{0},$ at an angle of $45^{\circ}$ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem $t = v_{0} / g$
Aa. $\frac{m v_{0}^{3}}{2 \sqrt{2} g}$
Bb. $\frac{m v_{0}^{3}}{\sqrt{2} g}$
Cc. $\frac{3 m v_{0}^{3}}{\sqrt{2} g}$
Dd. $\frac{\sqrt{2} m v_{0}^{3}}{g}$