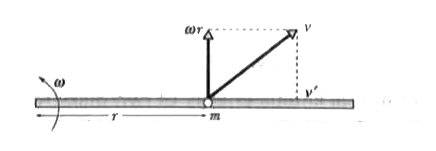
A smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.

Text Solution

Verified by Experts

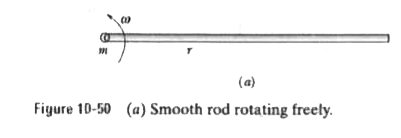
Consider the rod and the ring as our system. The system is experiencing no external torque about the axis hence, the angular momentum relative to the rotation axis does not vary. There is no nonconservative force or impulse acting so in the process of motion, the kinetic energy of the system does not vary.
Calculation: Since the angular momentum about the axis and kinetic energy of the system are conserved, we have
$I ω_{0} = (I + m r^{2}) ω$
and $\frac{1}{2} I ω_{0}^{2} = \frac{1}{2} I ω^{2} + \frac{1}{2} m v^{2}$
where $v^{2} = v .^{2} + ω^{2} r^{2}$ as shown in Fig. From the above two equations we obtain
$v = ω_{0} r / \sqrt{1 + m r^{2} / I}$
Note: If r = 0, we get v = 0 which is the situation in the beginning.

Updated on:21/07/2023

A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :

A $\frac{m l^{2}}{3}$
B $\frac{m l^{2}}{4}$
C $\frac{m l^{2}}{16}$
D $\frac{m l^{2}}{12}$
A thin rod of length $L$ of mass $M$ is bent at the middle point $O$ at an angle of $60^{\circ}$ . The moment of inertia of the rod about an axis passing through $O$ and perpendicular to the plane of the rod will be

A $\frac{M L^{2}}{6}$
B $\frac{M L^{2}}{12}$
C $\frac{M L^{2}}{24}$
D $\frac{M L^{2}}{3}$