A uniform rod of mass m and length l is hinged about one of its end. The hinge is smooth and rod lies on a smooth horizontal surface as shown in Fig. A particle of mass m is coming towards the rod at speed v0 perpendicular to the length of rod.
(a) Find angular velocity of the rod just after impact.

(b) Also find impulse due to hinge on rod during collision.
(a) (1) When the particle will hit the rod, the hinge will restrict the motion of the end of the rod. We can imagine the rod starting to rotate about hinge and particle continuing to move on same line of motion. The impulse that particle will experience by rod is along the line of motion.
(2) We will consider rod and particle as our system. This system will experience external impulse due to hinge. So, the momentum of the system cannot be conserved. But the angular momentum of the system about hinge will remain conserved as torque due to impulse at hinge is zero.
Calculation: By conserving angular momentum about hinge
mv0x=mvx+ml2ω3
Here v is the speed of particle after the collision and ω is the angular velocity of rod after the collision as shown in Fig. We can also write Newton.s law of collision remembering that it is the velocity of constant points that is required. Thus,
ωx−v0−v0=−e
Solving Eq. and,we get
ω=3v0x(1+e)(l2+3x2)
(b) (1) Coefficient of restitution is e and perpendicular distance of line of motion from hings is x. Consider e = 1/3, v0 = 3 m/s, l = 1 m, m = 2 kg and x = 1/3 m.
(2) Now to find impulse J1, due to the hinge, we will consider rod and particle as our system and write impulse and momentum equations.
Calculation: We should remember that impulse between rod and particle during the collision need not be considered since it will be in internal impulse, thus we can write
→J1=(→Prod f+→Pparticle f)−(→Prod i+→Pparticle i)
→Pparticle i=6Nm →Prod i=0
For →Pparticle.f we need to find speed of particle from part (a).
ω=3×3×(1/3)(1+1/3)[12+3(1/3)2]
Now solving for v by putting value of ω, we get
3×(1/3)−v0−(3)=−13m/s
Solving for v = 0, we get →Pparticle.f=0.
For →Prod.f we need velocity of center of mass of rod as
→Prod.f=MVcom.
Thus, Vcom=ω×rc=ω×l2=32m/s
and Prod f=2×32=3kgm/s
Hence, J1=(3+0)−(0+6)=−3kgm/s
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod in-elastically at its free end. Find out the angular velocity of the rod just after collision?

View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View Solution
Knowledge Check
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collisionAMvM+mBmvM+mC2mvM+mD2MvM+mA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 A6v05LB12v05LC2v05LD3v07L
A6v05LB12v05LC2v05LD3v07L
A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
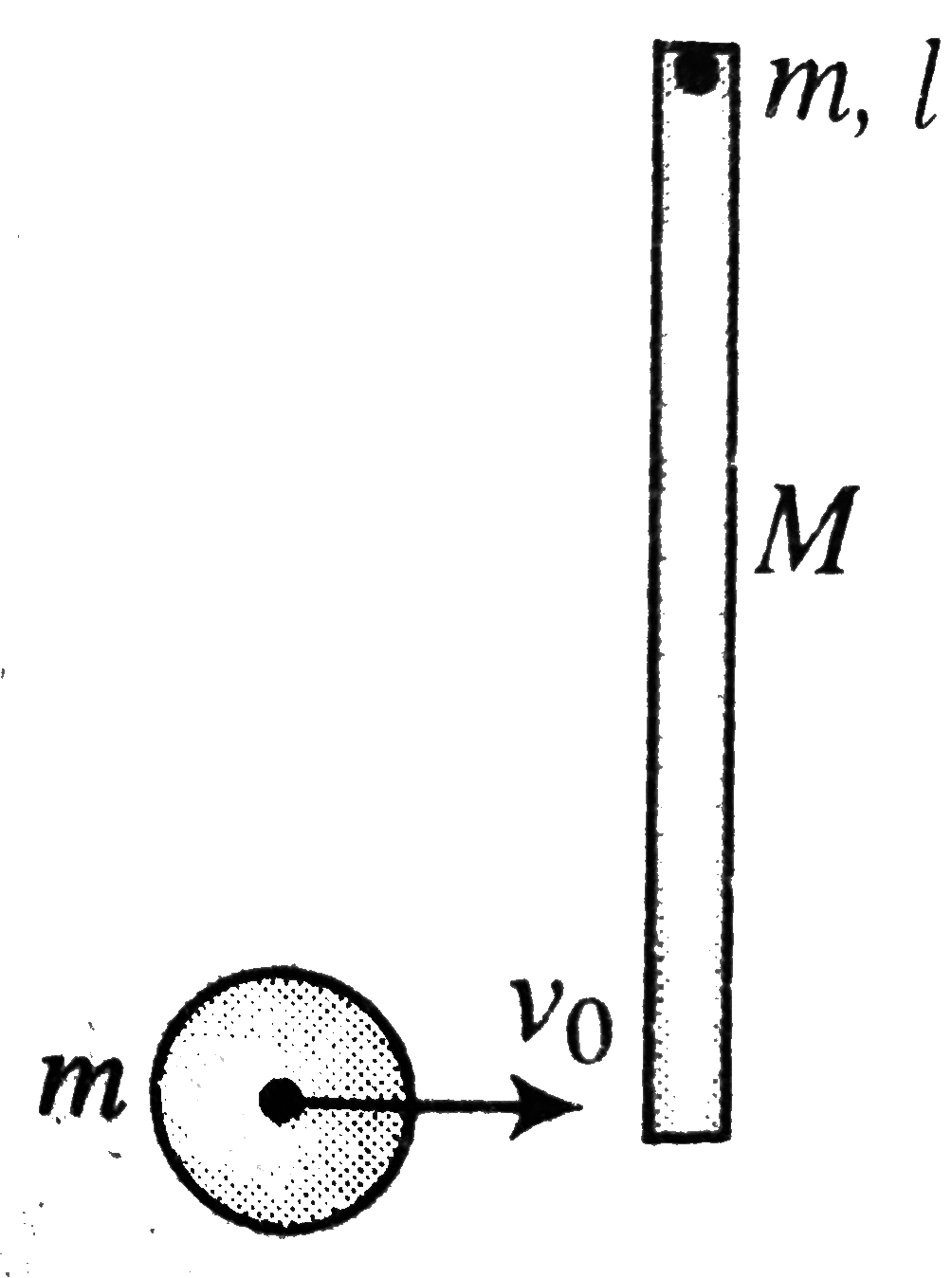
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)

View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View Solution
