A certain merry-go-round is accelerated uniformly from rest and attains an angular speed of 0.4 rad/s in the first 10 s. If the net applied torque is 2000 N⋅m, what is the moment of inertia of the merry-go-round?
400kg⋅m2
800kg⋅m2
50000kg⋅m2
5000kg⋅m2
The correct Answer is:C
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given data
- Initial angular velocity (ω0) = 0 rad/s (since it starts from rest)
- Final angular velocity (ωf) = 0.4 rad/s
- Time (t) = 10 s
- Net applied torque (τ) = 2000 N·m
Step 2: Calculate the angular acceleration (α)
We can use the formula for angular acceleration:
α=Δωt
where Δω=ωf−ω0.
Substituting the values:
Δω=0.4rad/s−0rad/s=0.4rad/s
α=0.4rad/s10s=0.04rad/s2
Step 3: Use the torque equation to find the moment of inertia (I)
The relationship between torque, moment of inertia, and angular acceleration is given by:
τ=I⋅α
Rearranging this formula to solve for I:
I=τα
Step 4: Substitute the values into the equation
Substituting the values of torque and angular acceleration:
I=2000N⋅m0.04rad/s2
Step 5: Calculate the moment of inertia
Calculating the above expression:
I=20000.04=50000kg⋅m2
Conclusion
The moment of inertia of the merry-go-round is 50000kg⋅m2.
---
- Initial angular velocity (ω0) = 0 rad/s (since it starts from rest)
- Final angular velocity (ωf) = 0.4 rad/s
- Time (t) = 10 s
- Net applied torque (τ) = 2000 N·m
We can use the formula for angular acceleration:
α=Δωt
where Δω=ωf−ω0.
Δω=0.4rad/s−0rad/s=0.4rad/s
α=0.4rad/s10s=0.04rad/s2
The relationship between torque, moment of inertia, and angular acceleration is given by:
τ=I⋅α
Rearranging this formula to solve for I:
I=τα
Substituting the values of torque and angular acceleration:
I=2000N⋅m0.04rad/s2
Calculating the above expression:
I=20000.04=50000kg⋅m2
The moment of inertia of the merry-go-round is 50000kg⋅m2.
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A cylinder of length 20cm and radius 10cm is rotating about its central axis at an angular speed of 100rad/s. What tangential force will stop the cylinder at a unifrom rate is 10s ? Given moment of inertia of the cylinder about its axis of rotation is 8.0kgm2.
View SolutionA torque of 2.0×10−4 Nm is applied to produce an angular acceleration of 4rad s−2 in a rotating body. What is the moment of inertia of the body ?
View Solution
Knowledge Check
A torque of 100 N-m acting on a wheel at rest, rotates it through 200 radian in 10 s. What is the moment of inertia of the wheel?
A10 kg-m2B15 kg-m2C20 kg-m2D25 kg-m2A child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)
 A2.0 rad/sB2.2 rad/sC2.4 rad/sD2.8 rad/s
A2.0 rad/sB2.2 rad/sC2.4 rad/sD2.8 rad/sA wheel starts from rest and attains an angular velocity of 20 radian/s after being uniformly accelerated for 10 s. The total angle in radian through which it has turned in 10 second is
A20πB40πC100D100π
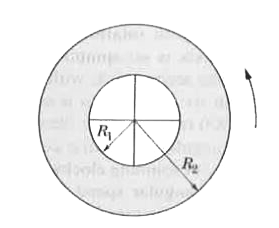
Figure 10-81 shows an overhead view of a ring that can rotate about its center like a merry-go-round. Its outer radius R2 is 0.800 m, its inner radius R1 is R2/2.00, its mass M is 6.00 kg, and the mass of the crossbars at its center is negligible. It initially rotates at an angular speed of 8.00 rad/s with a cat of mass m = M/4.00 on its outer edge, at radius R2. By how much does the cat increase the kinetic energy of the cat-ring system if the cat crawls to the inner edge, at radius R1?
View SolutionA block of mass 10 kg accelerates uniformly from rest to a speed of 2 m/s in 20 s. The average power developed in time interval of 0 to 20 seconds is :
View SolutionTwo disks are rotating about the same axis. Disk A has a moment of inertia of 3.4kg−m2 and an angular velocity of +72rad/s. Disk B is rotating with an angular velocity of −9.8rad/s. The two disks are then linked together without the aid of any external torques, so that they rotate as a single unit with an angular velocity of −2.4rad/s. The axis of rotation for this unit is the same as that for the separate disks. What is the moment of inertia of disk B?
View SolutionA playground merry-go-round is at rest, pivoted about a frictionless axis. A child of mass m runs along a path tangential to the rim with speed v and jumps on to the merry-go-round. If R is the radius of the merry-go-round and I is its moment of inertia, then the angular velocity of the merry-go-round is
View SolutionA boy is siting on a merry-go-round which is moving with a constant speed of 10 ms−1 . The means that the boy is :
View Solution
