एक व्यक्ति (द्रव्यमान = M),L लम्बाई के एक झूले पर झूल रहा है। झूले का कोणीय आयाम θ0 है। झूले के अपने निम्नतम बिन्दु से गुजरते समय, वह व्यक्ति झूले पर खड़ा हो जाता है। यदि खड़े होने से उस व्यक्ति का द्रव्यमान केन्द्र l(l<<L) दूरी से विस्थापित हो जाता है, तो, व्यक्ति द्वारा किया गया कार्य होगा
Mgl
Mgl(1+θ20)
Mgl(1−θ20)
Mgl(1+θ202)
The correct Answer is:B
कोणीय संवेग संरक्षण से,
Mv0L=Mv1(L−l)
v1=v0(LL−l)
ws+wp=ΔKE br> −mgl+wp=12m(v21−v20)
wp=mgl+12mv20((LL−l)2−1))
=mgl+12mv06(2)((1−lL)−2−1)
अब l<<1
द्विपद निकटता के अनुसार
=mgl+12mv20((1+2lL)−1)
=mgl+12mv20(2lL)
Wp=mgl+mv20lL
v0= अधिकतम वेग
=ω×A
=(√gL)(θ0L)
v0=θ0√gL
अतः wp=mgl+m(θ0√gL)2lL
=mgl(1+θ20).
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - GRAPHICAL QUESTIONS
6 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - JEE SECTION
36 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - नत समतल पर घूर्ण
21 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
एक जेट इंजन के परीक्षण के दौरान, उसका संपीडक (Compressor) निम्न ग्राफ के अनुसार चक्रण करता है। परीक्षण के दौरान संपीडक द्वारा पूर्ण किये गये चक्करों की संख्या होगी
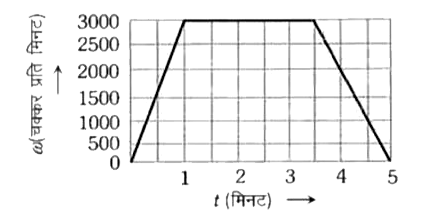
View Solutionएक स्थिर क्षैतिज समतल पृष्ठ पर एक गोला बिना फिसले लुढ़क रहा है। चित्र में, A तल से सम्पर्क बिन्दु, B गोले का केन्द्र तथा C उसका सबसे ऊपरी बिन्दु है, तब
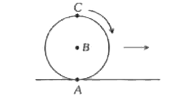
View Solutionएक गोला θ नति वाले नत समतल पर नीचे की ओर लुढ़क रहा है। तली पर पहुंचने पर गोले का त्वरण होगा
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionविकल्प में से सही विकल्प चुनकर वाक्य फिर से लिखिए :
सावन के झूले पर झूलती थीं ___________ |
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View SolutionIf a person travels from a point L towards east for 12 km and then travels 5 km towards north and reaches a point M, then shortest distance from L to M is: यदि एक व्यक्ति बिन्दु L से पूर्व की ओर 12 किमी. और फिर उत्तर की ओर 6 किमी, यात्रा करता है तो बिन्दु M पर पहुँचता है, तो L से M की न्यूनतम दूरी है
View Solutionएक संस्कृत व्यक्ति किसी चीज़ की खोज करता है, किन्तु उसकी संतान को वह अपने पूर्वजों से अनायास प्राप्त हो जाती है। जिस व्यक्ति की बुद्धि ने अथवा उसके विवेक ने किसी भी नए तथ्य का दर्शन किया, वह व्यक्ति ही वास्तविक संस्कृत व्यक्ति है और उसकी संतान जिसे अपने पूर्वज से वह वस्तु अनायास ही प्राप्त हो गई है, वह अपने पूर्वज की भांति सभ्य भले ही बन जाए, संस्कृत नहीं कहला सकती। एक आधुनिक उदाहरण लें। न्यूटन ने गुरुत्वाकर्षण के सिद्धांत का आविष्कार किया। वह संस्कृत मानव था। आज के युग का भौतिक विज्ञान का विद्यार्थी न्यूटन के गुरुत्वाकर्षण से तो परिचित है ही, लेकिन उसके साथ उसे और भी अनेक बातों का ज्ञान प्राप्त है, जिनसे शायद न्यूटन अपरिचित रहा। ऐसा होने पर भी हम आज के भौतिक विज्ञान के विद्यार्थी को न्यूटन की अपेक्षा अधिक सभ्य भले ही कह सकें, पर न्यूटन जितना संस्कृत नही कह सकते।
"संस्कृत' का अर्थ है
View Solutionएक संस्कृत व्यक्ति किसी चीज़ की खोज करता है, किन्तु उसकी संतान को वह अपने पूर्वजों से अनायास प्राप्त हो जाती है। जिस व्यक्ति की बुद्धि ने अथवा उसके विवेक ने किसी भी नए तथ्य का दर्शन किया, वह व्यक्ति ही वास्तविक संस्कृत व्यक्ति है और उसकी संतान जिसे अपने पूर्वज से वह वस्तु अनायास ही प्राप्त हो गई है, वह अपने पूर्वज की भांति सभ्य भले ही बन जाए, संस्कृत नहीं कहला सकती। एक आधुनिक उदाहरण लें। न्यूटन ने गुरुत्वाकर्षण के सिद्धांत का आविष्कार किया। वह संस्कृत मानव था। आज के युग का भौतिक विज्ञान का विद्यार्थी न्यूटन के गुरुत्वाकर्षण से तो परिचित है ही, लेकिन उसके साथ उसे और भी अनेक बातों का ज्ञान प्राप्त है, जिनसे शायद न्यूटन अपरिचित रहा। ऐसा होने पर भी हम आज के भौतिक विज्ञान के विद्यार्थी को न्यूटन की अपेक्षा अधिक सभ्य भले ही कह सकें, पर न्यूटन जितना संस्कृत नही कह सकते।
वास्तविक संस्कृत व्यक्ति वह है जो
View Solutionएक संस्कृत व्यक्ति किसी चीज़ की खोज करता है, किन्तु उसकी संतान को वह अपने पूर्वजों से अनायास प्राप्त हो जाती है। जिस व्यक्ति की बुद्धि ने अथवा उसके विवेक ने किसी भी नए तथ्य का दर्शन किया, वह व्यक्ति ही वास्तविक संस्कृत व्यक्ति है और उसकी संतान जिसे अपने पूर्वज से वह वस्तु अनायास ही प्राप्त हो गई है, वह अपने पूर्वज की भांति सभ्य भले ही बन जाए, संस्कृत नहीं कहला सकती। एक आधुनिक उदाहरण लें। न्यूटन ने गुरुत्वाकर्षण के सिद्धांत का आविष्कार किया। वह संस्कृत मानव था। आज के युग का भौतिक विज्ञान का विद्यार्थी न्यूटन के गुरुत्वाकर्षण से तो परिचित है ही, लेकिन उसके साथ उसे और भी अनेक बातों का ज्ञान प्राप्त है, जिनसे शायद न्यूटन अपरिचित रहा। ऐसा होने पर भी हम आज के भौतिक विज्ञान के विद्यार्थी को न्यूटन की अपेक्षा अधिक सभ्य भले ही कह सकें, पर न्यूटन जितना संस्कृत नही कह सकते।
सभ्य व्यक्ति वह है जो
View Solutionएक संस्कृत व्यक्ति किसी चीज़ की खोज करता है, किन्तु उसकी संतान को वह अपने पूर्वजों से अनायास प्राप्त हो जाती है। जिस व्यक्ति की बुद्धि ने अथवा उसके विवेक ने किसी भी नए तथ्य का दर्शन किया, वह व्यक्ति ही वास्तविक संस्कृत व्यक्ति है और उसकी संतान जिसे अपने पूर्वज से वह वस्तु अनायास ही प्राप्त हो गई है, वह अपने पूर्वज की भांति सभ्य भले ही बन जाए, संस्कृत नहीं कहला सकती। एक आधुनिक उदाहरण लें। न्यूटन ने गुरुत्वाकर्षण के सिद्धांत का आविष्कार किया। वह संस्कृत मानव था। आज के युग का भौतिक विज्ञान का विद्यार्थी न्यूटन के गुरुत्वाकर्षण से तो परिचित है ही, लेकिन उसके साथ उसे और भी अनेक बातों का ज्ञान प्राप्त है, जिनसे शायद न्यूटन अपरिचित रहा। ऐसा होने पर भी हम आज के भौतिक विज्ञान के विद्यार्थी को न्यूटन की अपेक्षा अधिक सभ्य भले ही कह सकें, पर न्यूटन जितना संस्कृत नही कह सकते।
'विद्यार्थी' शब्द का संधि-विच्छेद है
View Solutionएक संस्कृत व्यक्ति किसी चीज़ की खोज करता है, किन्तु उसकी संतान को वह अपने पूर्वजों से अनायास प्राप्त हो जाती है। जिस व्यक्ति की बुद्धि ने अथवा उसके विवेक ने किसी भी नए तथ्य का दर्शन किया, वह व्यक्ति ही वास्तविक संस्कृत व्यक्ति है और उसकी संतान जिसे अपने पूर्वज से वह वस्तु अनायास ही प्राप्त हो गई है, वह अपने पूर्वज की भांति सभ्य भले ही बन जाए, संस्कृत नहीं कहला सकती। एक आधुनिक उदाहरण लें। न्यूटन ने गुरुत्वाकर्षण के सिद्धांत का आविष्कार किया। वह संस्कृत मानव था। आज के युग का भौतिक विज्ञान का विद्यार्थी न्यूटन के गुरुत्वाकर्षण से तो परिचित है ही, लेकिन उसके साथ उसे और भी अनेक बातों का ज्ञान प्राप्त है, जिनसे शायद न्यूटन अपरिचित रहा। ऐसा होने पर भी हम आज के भौतिक विज्ञान के विद्यार्थी को न्यूटन की अपेक्षा अधिक सभ्य भले ही कह सकें, पर न्यूटन जितना संस्कृत नही कह सकते।
'पूर्वज' का विलोम शब्द है
View Solutionएक संस्कृत व्यक्ति किसी चीज़ की खोज करता है, किन्तु उसकी संतान को वह अपने पूर्वजों से अनायास प्राप्त हो जाती है। जिस व्यक्ति की बुद्धि ने अथवा उसके विवेक ने किसी भी नए तथ्य का दर्शन किया, वह व्यक्ति ही वास्तविक संस्कृत व्यक्ति है और उसकी संतान जिसे अपने पूर्वज से वह वस्तु अनायास ही प्राप्त हो गई है, वह अपने पूर्वज की भांति सभ्य भले ही बन जाए, संस्कृत नहीं कहला सकती। एक आधुनिक उदाहरण लें। न्यूटन ने गुरुत्वाकर्षण के सिद्धांत का आविष्कार किया। वह संस्कृत मानव था। आज के युग का भौतिक विज्ञान का विद्यार्थी न्यूटन के गुरुत्वाकर्षण से तो परिचित है ही, लेकिन उसके साथ उसे और भी अनेक बातों का ज्ञान प्राप्त है, जिनसे शायद न्यूटन अपरिचित रहा। ऐसा होने पर भी हम आज के भौतिक विज्ञान के विद्यार्थी को न्यूटन की अपेक्षा अधिक सभ्य भले ही कह सकें, पर न्यूटन जितना संस्कृत नही कह सकते।
'अनायास' का अर्थ है
View Solution
