Draw a ray diagram showing the formation of the image by a point object on the principal axis of a spherical convex surface separating two media of refractive indices $n_{1}$ and $n_{2}$ , when a point source is kept in rarer medium of refractive index $n_{1}$ . Derive the relation between object and image distance in terms of refractive index of the medium and radium of curvature of the surface.
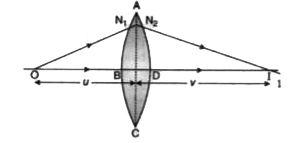
Hence obtain the expression for lens-maker's formula in the case of thin convex lens. Solution in Kannada

Video Solution

Text Solution

Verified by Experts

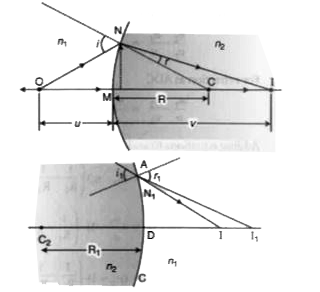
The incident rays coming from the object .O. kept in the rarer medium of refractive index $n_{1}$ , incident on the refracting surface NM produce the real image at I.
From the diagram,
$∠ i = ∠ N O M + ∠ N C M$
$= \frac{N M}{O M} + \frac{N M}{M C}$
$∠ r = ∠ N C M - ∠ N I M$
$= \frac{N M}{M C} - \frac{N M}{M I}$
From Snell.s law,
$∴ \frac{n_{2}}{n_{1}} = \frac{sin i}{sin r} ~ \frac{i}{r}$ ( for small angles, sin $θ ~ θ)$
$∴ n_{2} r = n_{1} i$
or $n_{2} (\frac{N M}{M C} - \frac{N M}{M I}) = n_{1} (\frac{N M}{O M} + \frac{N M}{M C})$
or $n_{2} (\frac{1}{+ R} - \frac{1}{+ v}) = n_{1} (\frac{1}{- u} + \frac{1}{R})$
or $\frac{n_{2} - n_{1}}{R} = \frac{n_{2}}{v} - \frac{n_{1}}{u}$
Lens maker.s formula $:$

The first refracting surface ABC forms the image $I_{1}$ of the object O. The image $I_{1}$ acts as a virtual object for the second refracting surface ADC which forms the real image I as shown in the diagram.
$:$ . For refraction at ABC
$\frac{n_{2}}{v_{1}} - \frac{n_{1}}{u} = \frac{n_{2} - n_{1}}{R_{1}}$ ....(i)
For refraction at ADC
$\frac{n_{1}}{v} - \frac{n_{2}}{v_{1}} = \frac{n_{1} - n_{2}}{R_{2}}$ ....(ii)
Adding equations (i) and (ii) , we get
$\frac{n_{1}}{v} - \frac{n_{1}}{u} = (n_{2} - n_{1}) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$\frac{1}{v} - \frac{1}{u} = (\frac{n_{2}}{n_{1}} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$\frac{1}{f} = (μ_{21} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

OSWAAL PUBLICATION-RAY OPTICS AND OPTICAL INSTRUMENTS-TOPIC-1(LONG ANSWER TYPE QUESTIONS)

Home
Ask Doubt
Profile