Obtain an expression for the force between two straight parallel conductor carrying current. Hence define ampere.Solution in Kannada
Correct figure with direction of force and currents.
B=μ02π⋅I1r
F=BI2lsinθ,θ=90∘
Fl=μ02π⋅I1I2r
Definition of ampere
Detailed answer:
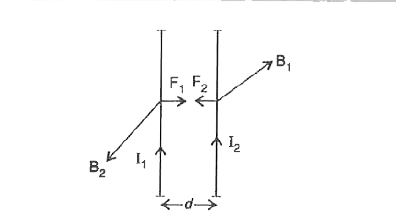
Consider two infinitely long parallel conductors carrying currents I1andI2 in the same direction.
Let .d. be the distance of separation between these two conductors.
The current I1, in the conductor (1) produces a magnetic field around it as shown in figure
The magnetic field at any point on the conductor (2) due to current I1 in conductor (1) is given by
B1=μO4π(2I1d)
The direction of B1 with reference to conductor (2) is perpendicular to the plane of the conductor and is directed vertically downward (i.e., into the plane)
We know, a current carrying conductor of length .l. placed at right angle to the magnetic field (B) experiences a force. which is given by
F=Bil
Therefore, force experienced per unit length of Conductor (2) in the magnetic field B1 is given by
F2=B1I1
=μO4π(2I1d)I2
=μO4π2I1I2d
By applying Fleming.s left hand rule to conductor (2) the direction of F2 is in the plane of the conductor is directed towards conductor (1)
Similarly F1=μO4π2I1I2d
Ampere is that current which if maintained in two infinitely long parallel conductors of negligible cross-section area separated by 1 metre in vacuum causes a force of 2×10−7N on each metre of the other wire.
Topper's Solved these Questions
- BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER (II PUC MARCH-2016)EXERCISE - PART-C8videos
SOLVED PAPER (II PUC MARCH-2016)
- BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER (II PUC JULY 2016)EXERCISE - PART D11videos
SOLVED PAPER (II PUC JULY 2016)
- BOOK - OSWAAL PUBLICATIONCHAPTER - SOLVED PAPER 1EXERCISE - Exercise39videos
SOLVED PAPER 1
Similar Questions
What is a transformer ? Mention two sources of energy loss in a transformer
05:15View SolutionDerive an expression for the electric field at a point due to an infinitely long thin charged straight wire using Gauss Law.
05:15View SolutionHow does the electrostatic force between two point charges change, when a dielectric medium is introduced between them ?
02:15View SolutionFind the force between two parallel conductors carrying currents (i) in the same direction (ii) in opposite directions and hence define one ampere.
11:28View SolutionDerive an expression for the force between two long parallel current carrying conductors. Use this expression to define SI unit of current.
10:04View SolutionUsing the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current between two infinitely long parallel current carrying conductors, define one ampere of current.
10:04View SolutionDerive an expression for the force acting between two very long parallel current-carrying conductors and hence define the Ampere.
10:04View SolutionObtain an expression for the force between two straight parallel conductor carrying current. Hence define ampere.
03:04View SolutionObtain an expression for the force between two straight parallel conductor carrying current. Hence define ampere.
10:04View SolutionObtain an expression for the force between two straight parallel conductors carrying current. Hence define ampere.
02:55View SolutionWrite the expression for force per unit length between two striaght parallel current carrying conductors of infinite length . Hence defin e SI unit of current 'ampere'.
05:51View SolutionObtain an expression for the force between two straight parallel conductor carrying current. Hence define ampere.
07:29View SolutionDerive an expression for the force per unit length between two infinitely long straight parallel current carrying wires. Hence, define one ampere (A).
04:19View SolutionDerive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
03:27View SolutionDerive an expression for the force between two long parallel current carrying conductors. Use this expression to define SI unit of current.
11:22View Solution

