A model of a ship is made to a scale of 1:200. If the length of the model is 4 m, the length of the ship is
200 m
800 m
80 m
20 m
The correct Answer is:B
To find the length of the actual ship based on the model's dimensions and the scale, we can follow these steps:
1. Understand the Scale: The scale of the model is given as 1:200. This means that 1 unit of measurement on the model corresponds to 200 units of measurement on the actual ship.
2. Identify the Length of the Model: The length of the model is given as 4 meters.
3. Set Up the Relationship: Using the scale, we can set up the relationship between the length of the model and the length of the actual ship. If we let L be the length of the ship, we can express this relationship as:
Length of ModelLength of Ship=1200
Substituting the known values, we have:
4 mL=1200
4. Cross-Multiply: To solve for L, we can cross-multiply:
4 m×200=1×L
This simplifies to:
800=L
5. Conclusion: Therefore, the length of the actual ship is:
L=800 m
Final Answer:
The length of the ship is 800 meters.
---
Length of ModelLength of Ship=1200
Substituting the known values, we have:
4 mL=1200
4 m×200=1×L
This simplifies to:
800=L
L=800 m
The length of the ship is 800 meters.
Similar Questions
A scale drawing of an object is the same shape at the object but a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio. The ratio of two corresponding sides in similar figures is called the scale factor.
Scale factor= length in image / corresponding length in object.
If one shape can become another using revising, then the shapes are similar. Hence, two shapes are similar when one can become the other after a resize, flip, slide or turn. In the photograph below showing the side view of a train engine. Scale factor is 1:200.

This means that a length of 1 cm on the photograph above corresponds to a length of 200cm or 2 m, of the actual engine. The scale can also be written as the ratio of two lengths.
If the length of the model is 11cm, then the overall length of theengine in the photograph above, including the couplings(mechanism used to connect) is:
View SolutionA model of a boat is made on the scale of 1:4. The model is 120cm long. The full size of the boat has a width of 60cm. What is the width of the scale model?

(i) 20 cm
(ii) 25 cm
(iii) 15 cm
(iv)240 cm
View Solution
Knowledge Check
In a model of a ship, the mast is 9cm high, while the mast of the actual ship is 12m high. If the length of the ship is 28m, how long is the model ship?
A21cmB22cmC20cmD26cmThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
A200 mB400 mC100 mD200√3mIf a ship of mass 4×107 kg initially at rest is pulled by a force of 5×104 N through a distance of 4 m, then the speed of the ship will be (resistance due to water is negligible )
A5ms−1B1.5ms−1C60ms−1D0.1ms−1
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 15 m high. If the length of the ship is 35 metres, how long is the model ship?
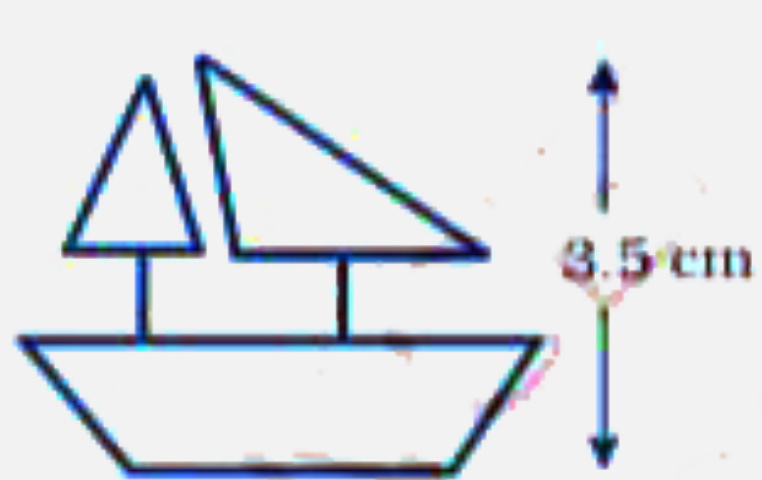
View SolutionThe model of a ship shown is of height 3.5 cm. The actual height of the ship is 210 cm if the scale chosen is 1: 60.
View SolutionThe resistance R to the motion of a ship depends on the velocity v of the ship, l the length of ship, ρ the density of sea water and g the acceleration due to the gravity.Show that R is proportional to l3.
View SolutionTwo ships are sailing in the sea on the two sides of a lighthouse. The angles of elevation of the top of the lighthouse as observed from the two ships are 30o and 45o respectively. If the lighthouse is 100 m high, the distance between the two ships is (a) 173 m (b) 200 m (c) 273 m (d) 300 m
View SolutionBelow you see a student's mathematical model of a farmhouse roof with measurements. The attic floor, ABCD in the model, is a square. The beams that support the roof are the edges of a rectangular prism, EFGHKLMN. E is the middle of AT, F is the middle of BT, G is the middle of CT, and H is the middle of DT. All the edges of the pyramid in the model have length of 12 m.
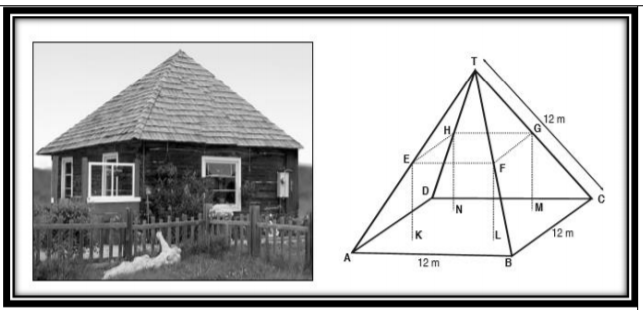
What is the length of EF, where EF is one of the horizontal edges of the block?
(i)24m
(ii)3m
(iii)6m
(iv)10m
View Solution
