In ΔPQR, D is the mid-point of ¯¯¯¯¯¯QR.then¯¯¯¯¯¯¯PM is ___________,PD is___________. Is QM=MR?
To solve the question step by step, let's analyze the triangle PQR with the given points and properties.
Step 1: Identify the Triangle and Midpoint
In triangle PQR, we know that D is the midpoint of the side QR. This means that the lengths of segments QD and DR are equal.
Hint: Remember that the midpoint divides a line segment into two equal parts.
Step 2: Define the Median
The segment PD is called a median. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Therefore, PD is the median of triangle PQR.
Hint: A median connects a vertex to the midpoint of the opposite side.
Step 3: Analyze the Segment PM
The problem states that PM is perpendicular to QR. This means that PM forms a right angle (90 degrees) with the line segment QR.
Hint: A perpendicular line creates a right angle with the line it intersects.
Step 4: Determine the Relationship of QM and MR
Since D is the midpoint of QR, we can conclude that QD = DR. However, the question asks if QM = MR. Since PM is perpendicular to QR, it does not bisect QR into two equal segments. Therefore, QM is not necessarily equal to MR.
Hint: A perpendicular line does not imply that it divides the opposite side into equal segments.
Final Answers
1. PM is a median.
2. PD is a median.
3. QM = MR? No, because PM is perpendicular and does not bisect QR.
In triangle PQR, we know that D is the midpoint of the side QR. This means that the lengths of segments QD and DR are equal.
The segment PD is called a median. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Therefore, PD is the median of triangle PQR.
The problem states that PM is perpendicular to QR. This means that PM forms a right angle (90 degrees) with the line segment QR.
Since D is the midpoint of QR, we can conclude that QD = DR. However, the question asks if QM = MR. Since PM is perpendicular to QR, it does not bisect QR into two equal segments. Therefore, QM is not necessarily equal to MR.
1. PM is a median.
2. PD is a median.
3. QM = MR? No, because PM is perpendicular and does not bisect QR.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle PQR, PQ=QR, A and B are the mid-points of ¯¯¯¯¯¯QR and ¯¯¯¯¯¯PR respectively. A circle passes through P,Q, A and B. Then which of the following is necessarily true?
A△ is equilateralB△ is right isoscelesCPQ is a diameterDBoth a) and c) - Question 2 - Select One
A ¯¯¯¯¯¯AB is 10.2 cm long. If P is the mid point of AB, then the length of ¯¯¯¯¯¯PB is ____
A4.8 cmB8.2 cmC5.1 cmD5.2 cm - Question 3 - Select One
If D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC)
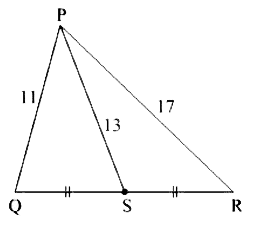
In ΔPQR, point S is the midoint of side QR. If PQ=11,PR=17,PS=13, Find QR.
 View Solution
View SolutionIn ΔPQR, point S is the midpoint of side QR. If PQ =11, PR =17 PS =13 , find QR.
View SolutionIn ΔPQR, if S is any point on side QR, show that PQ+QR+RP>2PS.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View Solution


