The equations of the circle which touches the axis of y at the origin and passes through (3, 4) , is
2(x2+y2)−3x=0
3(x2+y2)−25x=0
4(x2+y2)−25x=0
4(x2+y2)−25x+10=0
The correct Answer is:B
The centre of the circle lies on x-axis. Let a be the radius of the circle. Then, coordinates of the centre are (a, 0).
The circle passes through (3, 4). Therefore,
√(a−3)2+(0−4)2=a⇒−6a+25=0⇒a=256
So, the equation of the circle is (x−a)2+(y−0)2=a2
⇒x2+y2−2ax=0⇒3(x2+y2)−25x=0
(V) when the circle touches both the axes
In this case, we have h =k = a
Hence, the equation of the circle is
(x−a)2+(y−a)2=a2 or, x2+y2−2ax−2ay+a2=0
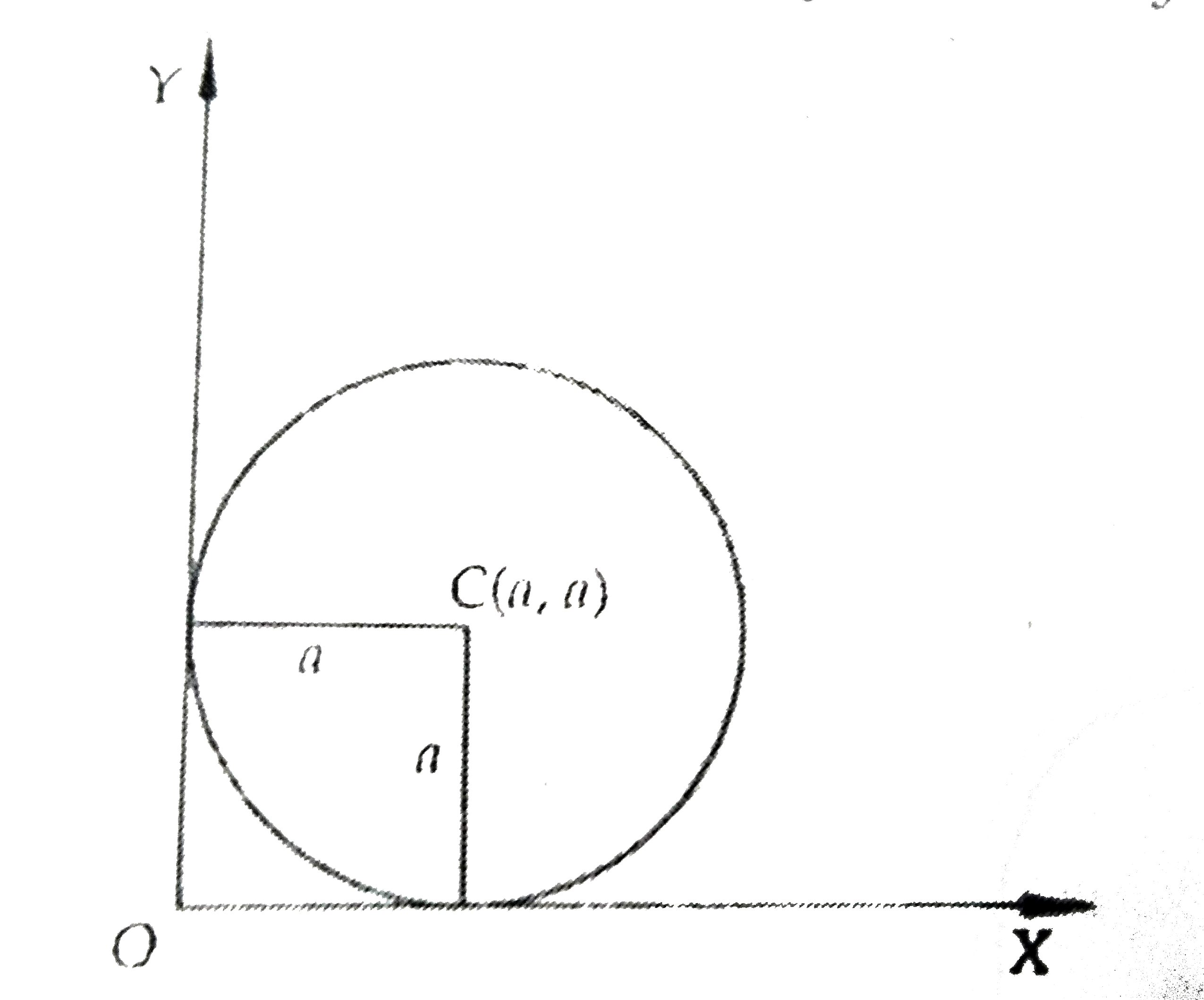
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Knowledge Check
Equation of circle which touches line x = y at the origin , and passes through (2,1), is
Ax2+y2+5x+5y=0Bx2+y2+5x−5y=0Cx2+y2−5x+5y=0Dx2+y2−5x−5y=0The equation of the circel which touches X-axis at (3,0) and passes through (1,4) is given by
Ax2+y2−6x−5y+9=0Bx2+y2+6x+5y−9=0Cx2+y2−6x+5y−9=0Dx2+y2+6x−5y+9=0
Find the equation of the circle which touches the axis of x and passes through the two points (1,-2) and (3,-4)
View SolutionFind the equation of the circle which touches the line x+8=0 at the point (−8,4) , and passes through the origin .
View SolutionThe equations of the circles which touch the y-axis at the origin and also the line 5x+12y−72=0 is
View SolutionFind the equation of the circle which touches the axis of y at a distance 4 from the origin and cuts off an intercept of length 6 on the axis of x.
View SolutionThe equation of the circle, which touches the parabola y2=4x at (1,2) and passes through the origin is :
View SolutionFind the radius of the circle which touches the axis of x at a distance 3 from the origin and cuts an intercept of length 6 on the axis of y.
View Solution
