A circle of radius 2 units touches the co ordinate axes in the first quadrant. If the circle makes a complete rotation on the x-axis along the positive direction of the x-axis, then the equation of the circle in the new position is
x2+y2−4(x+y)−8πx+(4π+1)2=0
x2+y2−4x−4y+(4π+2)2=0
x2+y2−8πx−4y+(4π+2)2=0
none of these
The correct Answer is:A
The old circle has centre at (2, 2) and at (2, 2) and radius 2. After one complete rotation on the x-axis in the positive direction of x-axis, the circle in its new position has centre at (4π+2,2) and same radius.
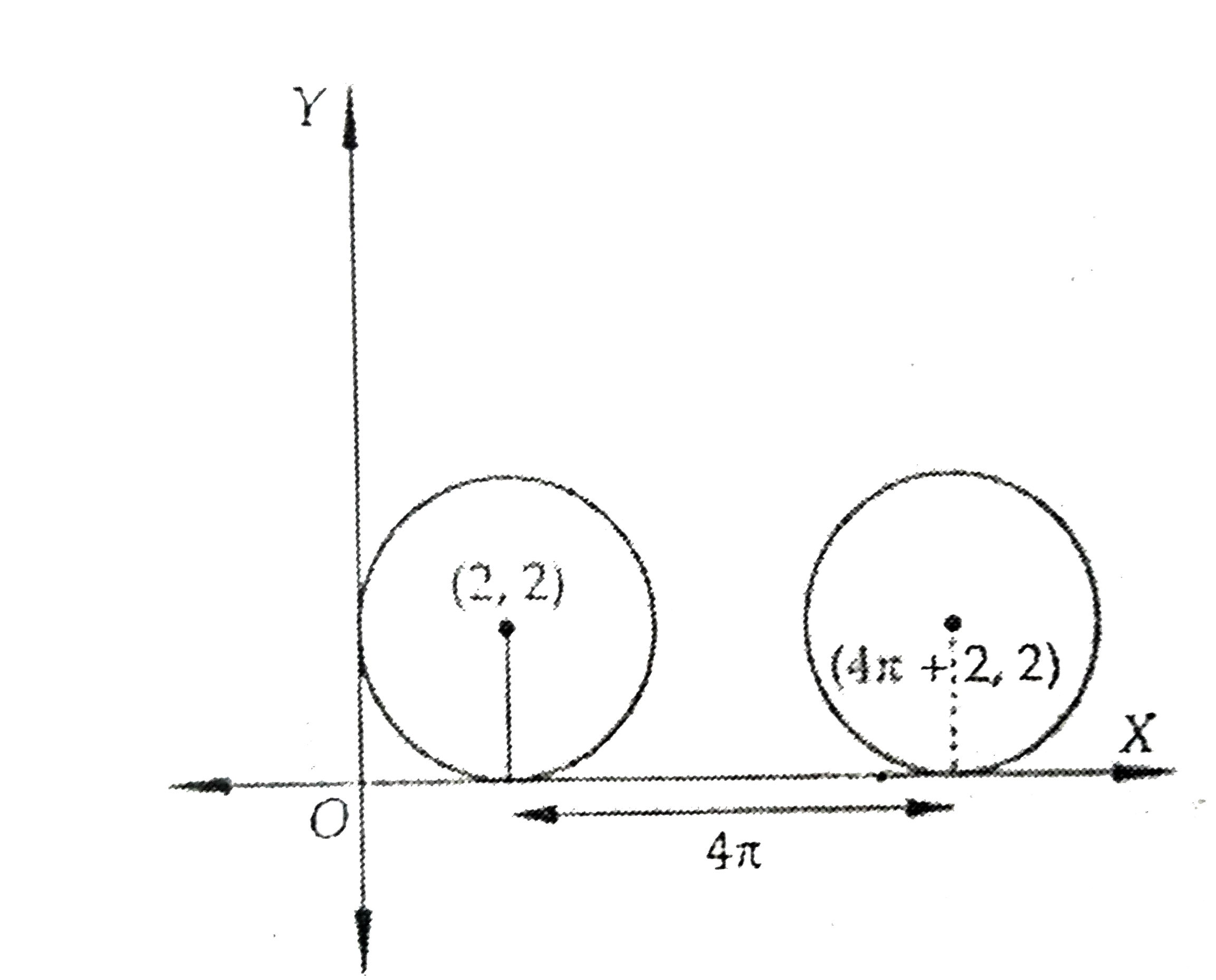
So, its equation is {x−(4π+2)}2+(y−2)2=22
⇒x2+y2−8πx−4(x+y)+(4π+2)2=0
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
A circle of radius 4 units touches the cordinate axes in the first quadrant. If the circle makes one compete roll on the x-axis along the positive direction of x-axis, find its equation in new position .
View SolutionA circle of radius 5units touches the coordinate axes in the first quadrant. If het circle makes one complete roll on x-a xi s along he positive direction of x-a xi s , find its equation in new position.
View Solution
Knowledge Check
A circle of radius 5 units touches both the axes and lies in the first quadrant. If the circle makes one complete roll on x-axis along the positive direction of x-axis, then its equation in the new position is
Ax2+y2+20πx−10y+100π2=0Bx2+y2+20πx+10y+100π2=0Cx2+y2−20πx−10y+100π2=0DNone of the aboveA circle of radius 5 units touches both the axes and lies in the first quadrant. If the circle makes one complete roll on x-axis along the positive direction of x-axis, then its equation in the new position is
Ax2+y2+20πx−10y+100π2=0Bx2+y2+20πx+10y+100π2=0Cx2+y2−20πx−10y+100π2=0Dnone of theseA circle touches y-axis at (0, 2) and has an intercept of 4 units on the positive side of x-axis. The equation of the circle, is
Ax2+y2−4(√2x+y)+4=0Bx2+y2−4(x+√2y)+4=0Cx2+y2−2(√2x+y)+4=0Dnone of these
A circle of radius 3 units touches both the axes in the first quadrant. Find its equation.
View SolutionA circle of radius 6 units touches the coordinates axes in the first quadrant. Find the equation of its image in the line mirror y=0.
View SolutionA circle of radius 4 units touches the cordinate axes in the first quadrant. Find the equation of its image in the line mirror y = 0 .
View SolutionA circle of radius 4 units touches the coordinate axes in the first quadrant. Find the equation of its images with respect to the line mirrors x=0 and y=0.
View SolutionA circle is drawn touching the x-axis and centre at the point which is the reflection of (a,b) to theline y−x=0 . The equation of the circle is
View Solution
