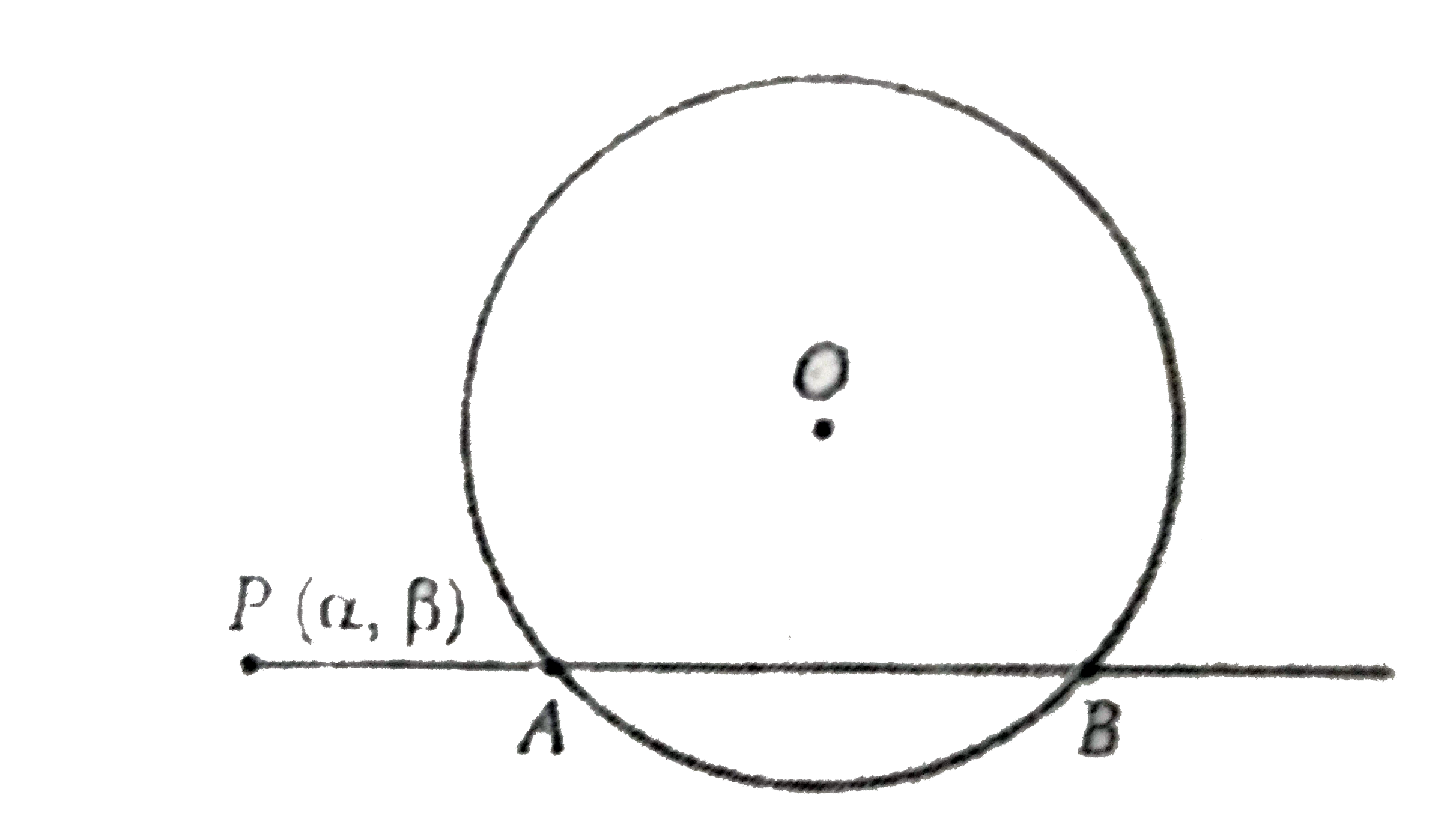
A line is drawn through a fix point P(α,β) to cut the circle x2+y2=r2 at A and B. Then PA.PB is equal to :
A
α2+β2
B
α2+β2−a2
C
a2
D
α2+β2+a2
Video Solution
Text Solution
The correct Answer is:C
The equation of any line through P(α,β) is
x−αcosθ=y−βsinθ
The coordinates of any point on this line at a distance r from P are (α+rcosθ,θ,β+rsinθ). If it lies on the given circle, then
(α+rcosθ)2+(β+rsinθ)2=a2
⇒r2+2r(αcosθ+βsinθ)+α2+β2−a2=0
This equation gives two values of r, say r1,r2 These two values are lengths PA and PB.
∴PA×PB=r1r2=α2+β2−a2
|
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Knowledge Check
A line is drawn through a fixed point P(α,B) to cut the circle x2+y2=r2 at A and B. Then PA.PB is equal to
A(α+β)2−r2B(α2+β2−r2C(α−β)2+r2DNone of the aboveA line is drawn through a fixed point P(h, k) to cut the circle x2+y2=a2 at A and B. Then PA, PB is equal to
A(h+k)2−a2Bh2+k2−a2C(h−k)2+a2Dnone of theseA line is drawn through the point P(3,11) to cut the circle x2+y2=9 at A and B. Then PA.PB is equal to
A9B121C205D139
The tangent at the point (α,β) to the circle x2+y2=r2 cuts the axes of coordinates in AandB. Prove that the area of the triangle OAB is a2r4|αβ|,O being the origin.
View SolutionIf a line passes through the point P(1,−2) and cuts the x2+y2−x−y=0at A and B, then themaxiμmofPA+PB is
View SolutionA line passing through the points A(1.−2) cuts the circle x2+y2−y=0 at PandQ. Then the maximum value of |AP−AQ| is
View SolutionA line is drawn through the point P(3,11) to cut the circle x2+y2=9 at A and B. Then, PA⋅PB is equal to
View SolutionA line passes through the point P(5,6) outside the circle x2+y2=12 and meets the circle at A and B. The value of PA. PB is equal to
View Solution
