If the distances from the origin of the centers of three circles x2+y2+2λx−c2=0,(i=1,2,3), are in GP, then prove that the lengths of the tangents drawn to them from any point on the circle x2+y2=c2 are in GP.
A.P.
G.P.
H.P.
none of these
The correct Answer is:B
The centres of the given circles are (−λi,0) (i=1, 2, 3).The distances from the origin of the centres are λ−(1),λ2 and λ3.
Let P(h, k) be any point on the circle x2+y2=c2. Then,
h2+k2=c2
Now,
Li = Length of the tangent from (h, k) to
x2+y2+1λixx−c2=0
⇒Li=√h2+k2+2λih−c2
⇒Li=√c2+2λih−c2 [∵h2+k2=c2]
⇒Li=√2,λih, i=1,2,3.
∴L22=2λ2h
⇒L22=2h(√2λ1λ3 [∵λ22=λ1λ3]
⇒L22=√2λ1h√2λ3h=L1L3
Hence, L1,L2,L3 are in G.P.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
If the distances from the origin of the centers of three circles x2+y2+2λx−c2=0,(i=1,2,3), are in GP, then prove that the lengths of the tangents drawn to them from any point on the circle x2+y2=c2 are in GP.
View SolutionThe length of the tangent drawn from the point (2,3) to the circle 2(x2+y2)−7x+9y−11=0.
View Solution
Knowledge Check
If the distances from the origin of the centres of the three circles x2+y2−2λix=c2(i=1,2,3) are in G.P., then the lengths of the tangents drawn to them from any point on the circle x2+y2=c2 are in
AA.P.BG.P.CH.P.Dnone of theseThe equation of tangents drawn from the point (0,1) to the circle x2+y2−4x−2y+4=0 are
A2x-y+1=0 ,x+2y-2=0B2x-y-1=0 ,x+2y-2=0C2x-y+1=0,x+2y+2=0Dx=±√3(y−1)The length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
A7B49C63D21
Prove that the lengths of the tangents from any point on the line 3x−8y+2=0 to the circles x2+y2−4x+6y+8=0 are equal
View SolutionThe length of the tangent from the point (1,2) to the circle 2x2+2y2+6x−8y+3=0 is ………. .
View SolutionFind the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
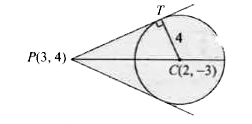
View SolutionThe length of the tangent drawn from the point (2, 3) to the circles 2(x2+y2)–7x+9y–11=0.
View SolutionThe equation of pair of tangents drawn from the point (0,1) to the circle x2+y2–2x+4y=0 is–
View Solution
