From the point P(3, 4) tangents PA and PB are drawn to the circle x2+y2+4x+6y−12=0. The area of Δ PAB in square units, is
132342
171574
92617
140913
The correct Answer is:B
Clearly , AB is the chord of contact of tangents drawn from P(3, 4) to the circle x2+y2+4x+6y−12=0.
Therefore, equation of AB is
3x+4y+2(x+3)+3(y+4)−12=0
⇒5x+7y+6=0
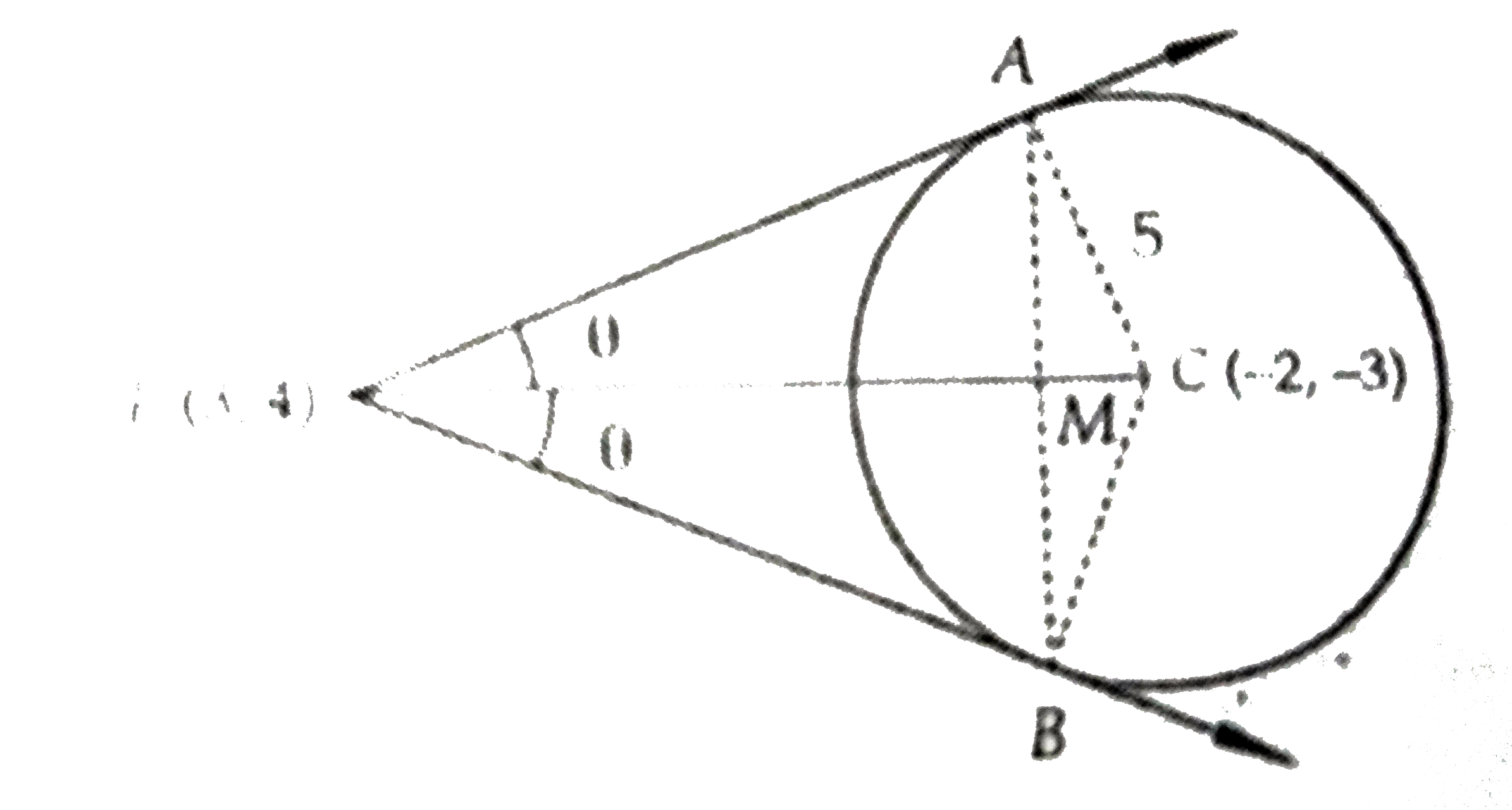
In ΔPAC, we have
tanθ=CAPA⇒tanθ=5√9+16+12+24−12=57
∴sin2θ=2tanθ1+tan2θ⇒sin2θ=7074
∴Area of ΔPAB=12×PA×PB×sin20
⇒Area of ΔPAB=12×7×7×7074sq. units=171574sq. units.
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Video
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
From the point P(4,−4) tangents PA and PB are drawn to the circle x2+y2−6x+2y+5=0 whose centre is C then Length of AB
View SolutionFrom the point P(√2,√6) , tangents PAandPB are drawn to the circle x2+y2=4 Statement 1 :The area of quadrilateral OAPB(O being the origin) is 4. Statement 2 : The area of square is a2, where a is the length of side.
View Solution
Knowledge Check
If tangents PA and PB are drawn from P(−1,2) to y2=4x then
AEquation of AB is y=x−1BLength of AB is 8CLength of AB is 4DEquation of AB is y=x+1Two tangents OA and OB are drawn to the circle x2+y2+4x+6y+12=0 from origin O. The circumradius of ΔOAB is :
A12B1C2D12√13From any arbitrary point P on the line +y = 4, tangents PA and PB are drawn to the circlex2+y2=8. Find the equation that satisfies the locus of the midpoint of AB.
Ax2+y2+2x+2y=0Bx2+y2−2x−2y=0Cx2+y2−2x+2y=0Dx2+y2+2x−2y=0
If tangents are drawn from origin to the circle x2+y2−2x−4y+4=0, then
View SolutionTangents PA and PB are drawn to the circle x2+y2=4,then locus of the point P if PAB is an equilateral triangle ,is equal to
View SolutionFrom point P(4,0) tangents PA and PB are drawn to the circle S:x2+y2=4. If point Q lies on the circle, then maximum area of △QAB is- (1) 2√3 (2) 3√3 (3) 4√3 A) 9
View SolutionFrom point P on the circle x2−y2−2x+6y−8=0. tangents PAandPB are drawn to the circle x2+y2−2x+6y+1=0, then the locus of orthocentre of ΔPAB is x2+y2+ax+by+c=0, where (a+b−c) is equal to -
View SolutionTangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
View Solution
