The length of the transversal common tangent to the circle x2+y2=1 and (x−t)2+y2=1 is √21, then t=
A
±2
B
±5
C
±3
D
none of these
Video Solution
Text Solution
The correct Answer is:B
If d is the distance between the centres of two circles of radii r1 and r2 , then
Length of transversal common tangent =√d2−(r1+r2)2
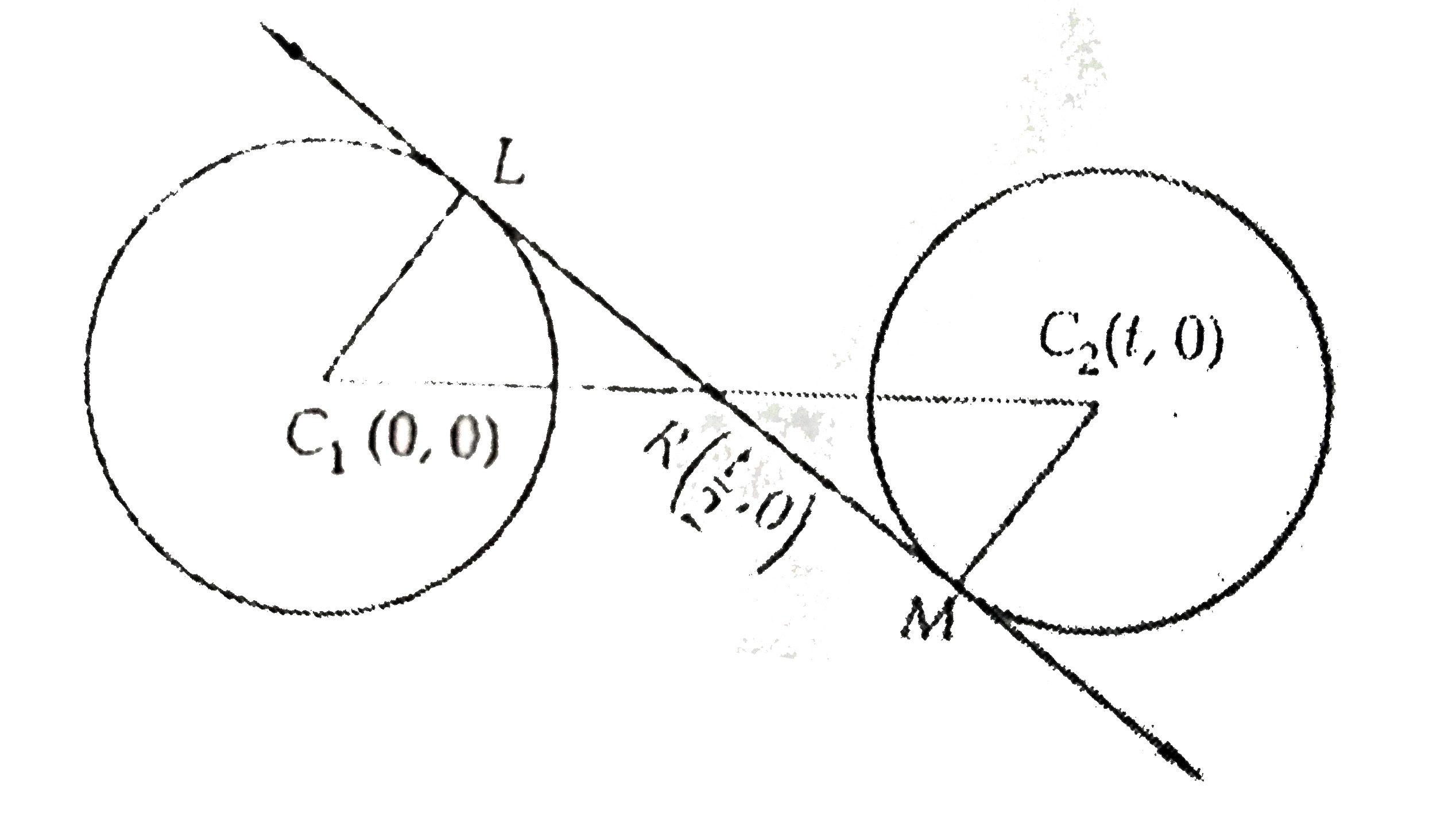
Centres of the given circles are C1(0,0) and C2(t,0) and corresponding radii are r1=1 and r2=1 respectively.
∴d=√(t−0)2+0=|t|
It is given that :
Length of transversal common tangent =√21
⇒√d2−(r1+r2)2=√21⇒t2−22=21⇒t=±5
ALITER–––––––––– Since given circles are of equal radius. Therefore, R is the mid-point of C1C2. Also , ΔC1LR≅ΔC2MR.
∴ R is the mid-point of LM.
In ΔC1LR, we have
C1R2=C1L2+LR2
⇒LR=√C1R2−C1L2=√t24−1=√t2−42
∴LM=√21
⇒2LR=√21⇒√t2−4=√21⇒t2=25⇒t=±5
|
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Knowledge Check
A common tangent to the circles x2+y2=4 and (x−3)2+y2=1, is
Ax=4By=2Cx+√3y=4Dx+2√2y=6The number of common tangents of the circles x2+y2=16 and x2+y2−2y=0 is :
A2B3C4D0The number of common tangents to the circles x2+y2−y=0andx2+y2+y=0 is
A2B3C0D1
The number of common tangents to the circles x2+y2−x=0andx2+y2+x=0 are
View SolutionTwo common tangents to the circle x2+y2=a2 and parabola y2=4a√2x are
View SolutionThe number of common tangents of the circles x2+y2+4x+1=0 and x2+y2−2y−7=0, is
View SolutionThe number of common tangents of the circles x2+y2=16 and x2+y2−2y=0 is :
View SolutionThe number of common tangents to the circles x2+y2−x=0,x2+y2+x=0 is
View Solution
