The common tangents to the circles x2+y2+2x=0andx2+y2−6x=0 form a triangle which is
A
equilateral
B
isosceles
C
right angled
D
none of these
Video Solution
Text Solution
The correct Answer is:B
Clearly, the distance between the centres of the given circles is equal to the sum of their radii. So, two given circles will touch each other externally.
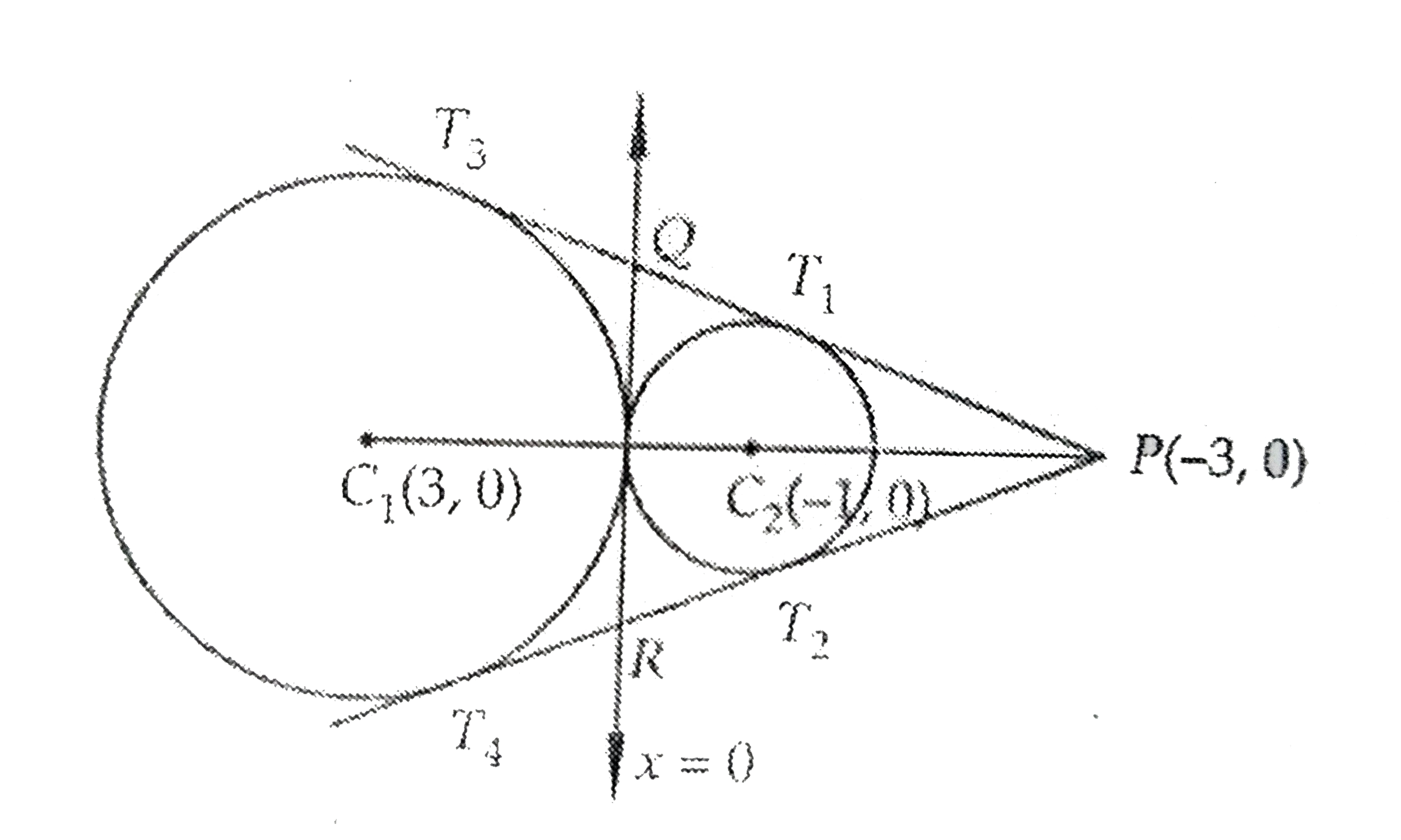
We have,
PT1=PT2andPT3=PT4
⇒T1T3=T2T4
⇒T1Q=T2R
⇒PT1+T1Q=PT1+T2R
⇒PT1+T1Q=PT2+T2R
⇒PQ=QR
Hence, ΔPQR is an isosceles triangle
|
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
Similar Questions
Knowledge Check
The common tangents to the circles x2+y2+2x=0 and x2+y2−6x=0 from a triangle which is :
AequilateralBisoscelesCright angledDnone of theseThe common tangents to the circles x2+y2+2x=0 and x2+y2−6x=0 from a triangle which is :
AequilateralBisoscelesCright angledDNone of theseThe circles x2+y2−6x−8y=0 and x2+y2−6x+8=0 are
Aintersecting in two pointsBnon-intersectingCtouching externallyDtouching internally
The number of common tangents to the circles x2+y2=4 and x2+y2−6x−8y−24=0 is
View SolutionFind the number of common tangents to the circles x2+y2=4 and x2+y2−6x−8y=24
View SolutionThe number of common tangents to the circles x2+y2−x=0,x2+y2+x=0 is
View SolutionThe number of common tangents of the circles x2+y2=16 and x2+y2−2y=0 is :
View SolutionThe number of common tangents to the circles x2+y2=4andx2+y2−6x−8y=24 is
View Solution
