The locus of the foot of the normal drawn from any point P(α,β) to the family of circles x2+y2−2gx+c=0, where g is a parameter, is

A

(x2+y2+c)(y−β)=2(ya−xβ)x

B

(x2+y2+c)(x−β)=2(yα−xβ)x

C

(x2+y2+c)(x−β)=2(xα−yβ)x

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Let A (h, k) be the foot of the normal drawn from P(α,β) to the given circle. Then, P, Q and C are collinear points.
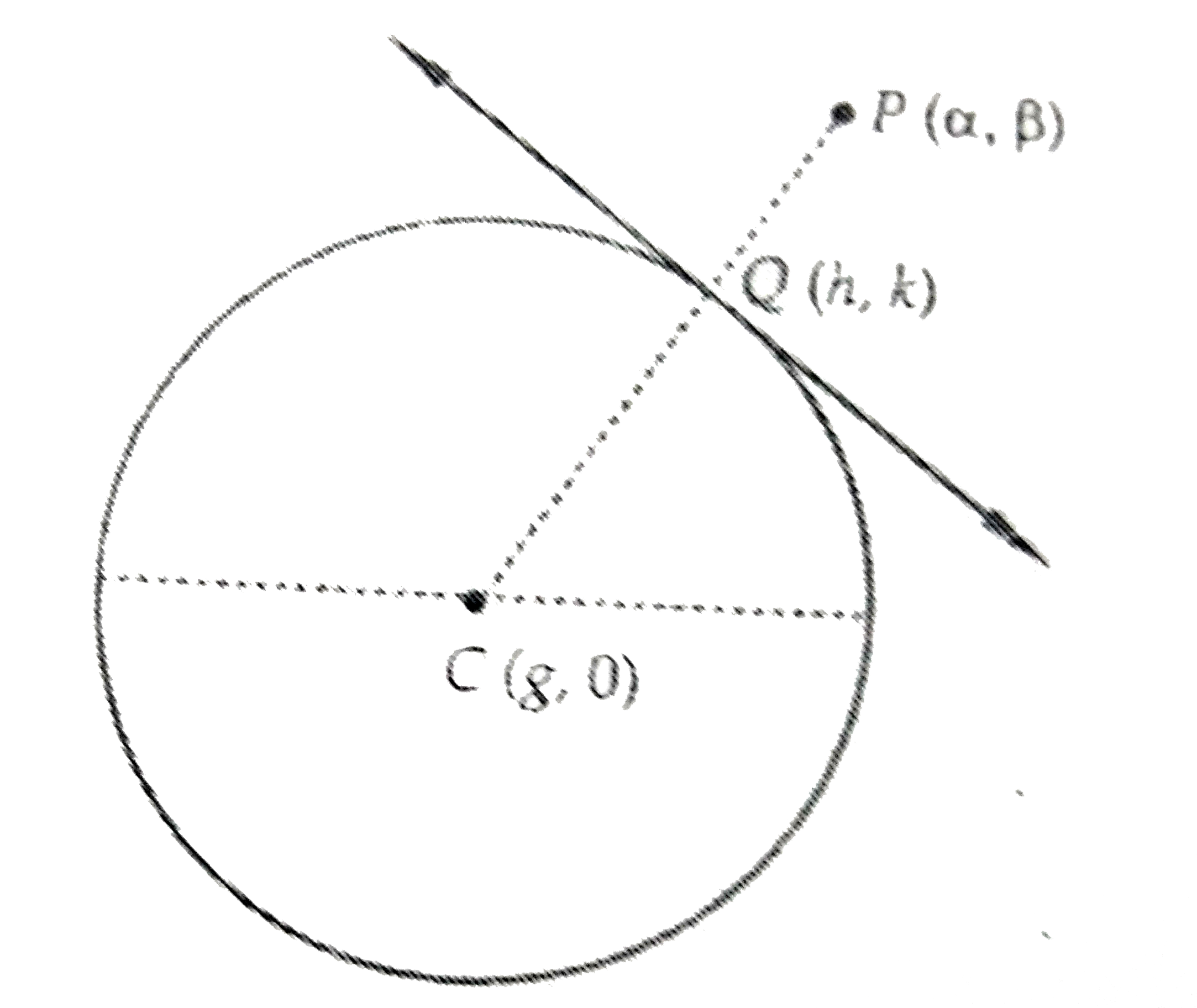
ocr_image
∣∣ ∣ ∣∣αβ1hk1g01∣∣ ∣ ∣∣=0
⇒αk+βg−βh−gk=0⇒g(β−k)=βh−αk ...(i)
Also, CQ=Radius
⇒(g−h)2+k2=g2−c
⇒−2gh+h2+k2=−c⇒g=h2+k2+c2h ...(ii)
From (i) and (ii), we get h2+k2+c2h=βh−αkβ−k
Hence, the locus of (h, k) is
(x2+y2+c)(β−y)=2(βx−αy)x
Thus, option (a) is correct.

Updated on:21/07/2023
|
Class 12MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The range of g so that we have always a chord of contact of tangents drawn from a real point (α,α) to the circle x2+y2+2gx+4y+2=0, is

    A(-3, 0)
    B(-4, 1)
    C(-4, 0)
    Dnone of these

  • The locus of the foot of the perpendicular drawn from the centre on any tangent to the ellipse x225+y216=1 is:

    A25x2+16y2=(x2+y2)2
    B25x2+16y2=9
    C16x2+25y2=1
    Dx2+y2=41

  • The locus of the foot of the perpendicular drawn from the origin to any tangent to the hyperbola x236−y216=1 is

    A(x2+y2)2=36x2−16y2
    B(x2−y2)2=36x2−16y2
    C(x2+y2)2=36x2+16y2
    D(x2−y2)2=36x2+16y2