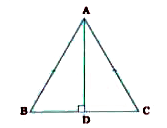
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that: ( i ) AD bisects BC ( ii) AD bisects ∠ A
 Solution in Gujrati
Solution in Gujrati
Step by step video & image solution for AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that: ( i ) AD bisects BC ( ii) AD bisects angle A by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Show that in a right angled triangle, the hypotenuse is the longest side.
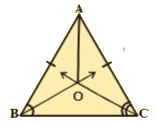
View SolutionIn an isosceles triangle ABC, with AB = AC, the bisectors of ∠Band∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC (ii) AO bisects ∠A
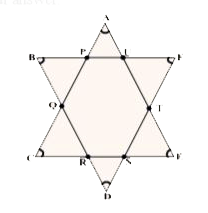
View SolutionWhat is the measure of ∠A+∠B+∠C+∠D+∠E+∠F in the figure given below. Give reason to your answer.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
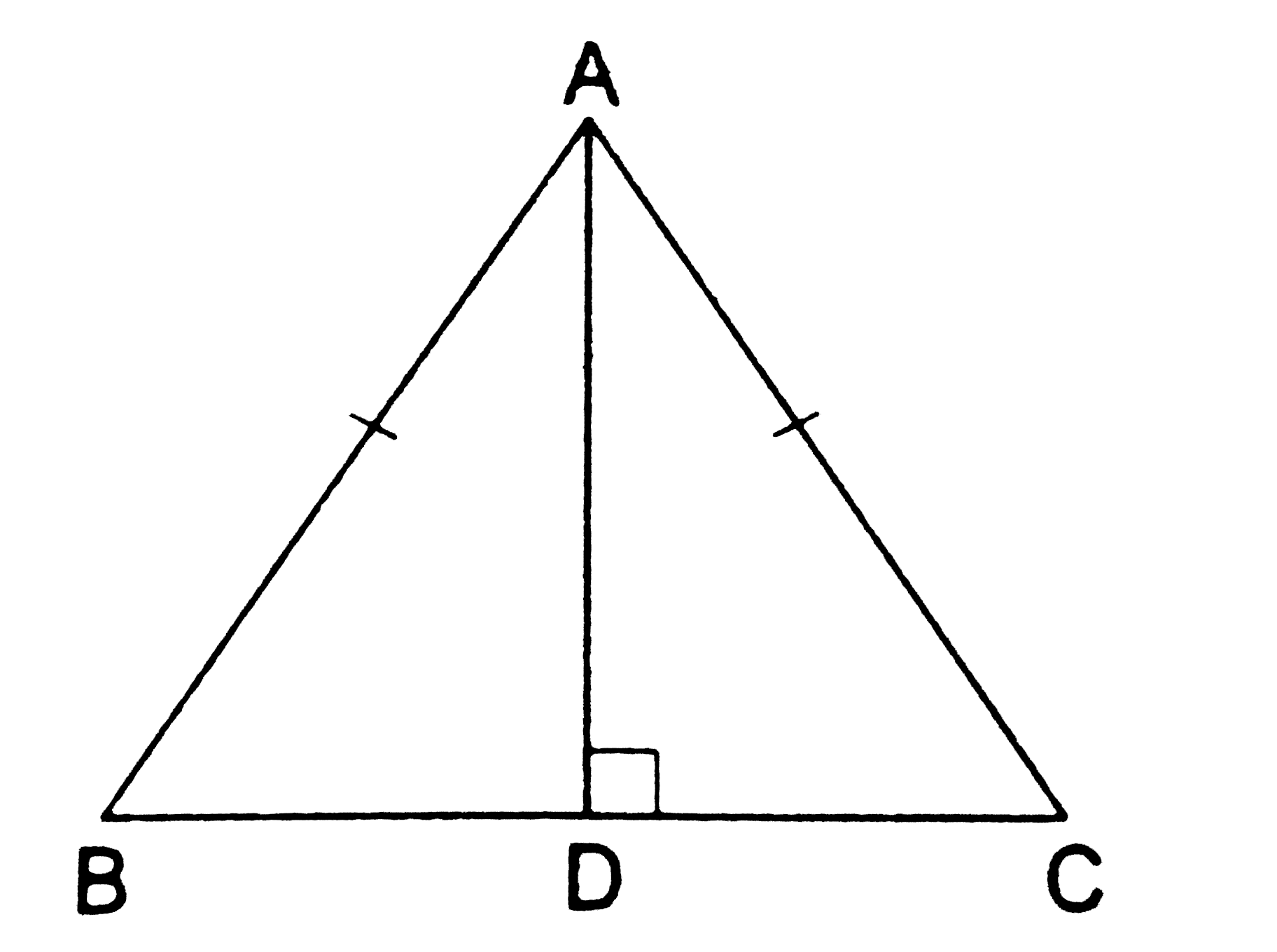
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
View SolutionAD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखाखंड BC को समद्विभाजित करता है। (ii ) AD कोण A को समद्विभाजित करता है।
View SolutionAD एक समद्विबाहु त्रिभुज ABC का एक सिर्शलम्ब है, जिसमे AB=AC है दर्शाइए की (i) AD रेखाखण्ड BC को समद्विभाजित करता है, (ii) AD कोण A को समद्विभाजित करता है
View SolutionAD is an altiude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
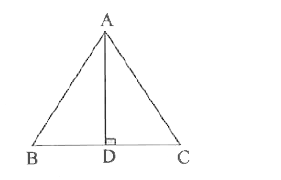
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD एक समद्धिबाहू त्रिहुज ABC का एक शीर्षलम्ब है, जिसमे AB -= AC है | दर्शाइए कि
(i) AD रेखाखण्ड BC को समद्धिभाजित करता है |
(ii) AD कोण A को समद्धिभाजित करता है |
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.

View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that: ( i ) AD bisects BC ( ii) AD bisects ∠ A

View Solution
