Two poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles. Solution in Gujrati
Step by step video & image solution for Two poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60^(@) and 30^(@) respectively. Find the height of the poles and the distances of the point from the poles. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF TRIGONOMETRYBOOK - NCERT GUJARATICHAPTER - APPLICATIONS OF TRIGONOMETRYEXERCISE - Optional Exercise (For extensive learning)
4 Videos
- APPLICATIONS OF TRIGONOMETRYBOOK - NCERT GUJARATICHAPTER - APPLICATIONS OF TRIGONOMETRYEXERCISE - THINK AND DISCUSS
1 Videos
- APPLICATIONS OF TRIGONOMETRYBOOK - NCERT GUJARATICHAPTER - APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise 12.1
10 Videos
- COORDINATE GEOMETRY BOOK - NCERT GUJARATICHAPTER - COORDINATE GEOMETRY EXERCISE - TRY THIS
10 Videos
Similar Questions
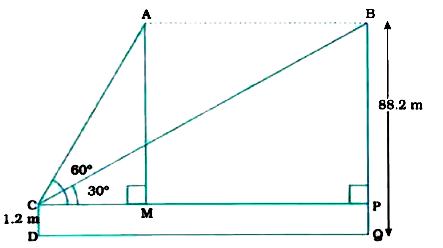
A 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘ (see the given figure). FInd the distance travelled by the balloon during the interval.
View SolutionA ladder of length x meter is leaning against a wall making angle θ with the ground. Which trigonometric ratio would you like to consider to find the height of the point on the wall at which the ladder is touching
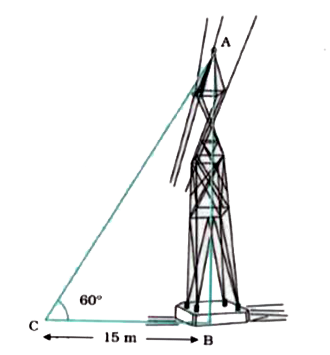
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60∘. Find the height of the tower.
View SolutionWhere do these following points lie (0, -3), (0, -8), (0, 6) and (0, 4) on coordinate plane?
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point P between them on the road, the angle of elevation of the top of one pole is 60∘ and the angle of depression from the top of another pole is 30∘ find the height of pole and distances of the point P from the poles.
View SolutionTwo poles of equal height are standing opposite to each other on either sidef of the road, which is 120 feet wide. From a point between then on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal height are standing opposite to each other on either side of the road, which is 80 m wide. From a point between then on the road, the angles of elevation of top of the poles are 60∘ and 30∘. Find the height of poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘, respectively . Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ to 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and 30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View SolutionTwo poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘ and 30∘ respectively. Find the height of the poles and the distances of the point from the poles.
View Solution
