A rectangle glass wedge (prism) is immersed in water as shown in figure E-a. For what value of angle α, will the beam of light, which is normally incident on AB, reach AC entirely as shown in figure E-b. Take the refractive index of water as 43 and the refractive index of glass as 32. 
From the geometry of figure E-b it is clear that, the angle of incidence on the side BC is equal to α (dotted line is a normal drawn at the point of incidence). The ray should undergo total internal reflection to reach AC. For occurrence of total internal reflection, the value of α must be greater than the critical angle at interface of water and glass. 
Let .C. be the critical angle of interface of glass and water. From the given condition α>C.......(1)
We know, sinC=1n12 ........(2)
n12=32/43=98
From equation 2, we get
sinC=89⇒C=62∘301
Hence α is greater than C=62∘301
Let us see few activities of total internal reflection.
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - NCERT GUJARATICHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - I. Reflections on Concepts
7 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - NCERT GUJARATICHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - II. Application of concepts
4 Videos
- MOTIONBOOK - NCERT GUJARATICHAPTER - MOTIONEXERCISE - THINK AND DISCUSS
14 Videos
- SOUNDBOOK - NCERT GUJARATICHAPTER - SOUNDEXERCISE - Let us Improve our learning (Multiple choice questions)
5 Videos
Similar Questions
Find the refractive index of water with respect to glass if the refractive index of water is 4/3 and the refractive index of glass is 3/2.
View SolutionA glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
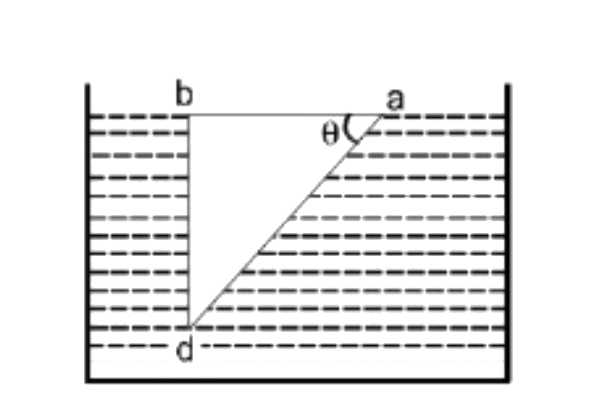
View Solution
Knowledge Check
Refractive index of glass is 32 and the refractive index of water is 43. Then the refractive index of glass with respect to water is
A3/24/3B32×43C32+43D32−43A glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
 Asinθ<(2/3)Bsinθ>(8/9)C(2/3)<sinθ<(8/9)DNone of these
Asinθ<(2/3)Bsinθ>(8/9)C(2/3)<sinθ<(8/9)DNone of theseA ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be
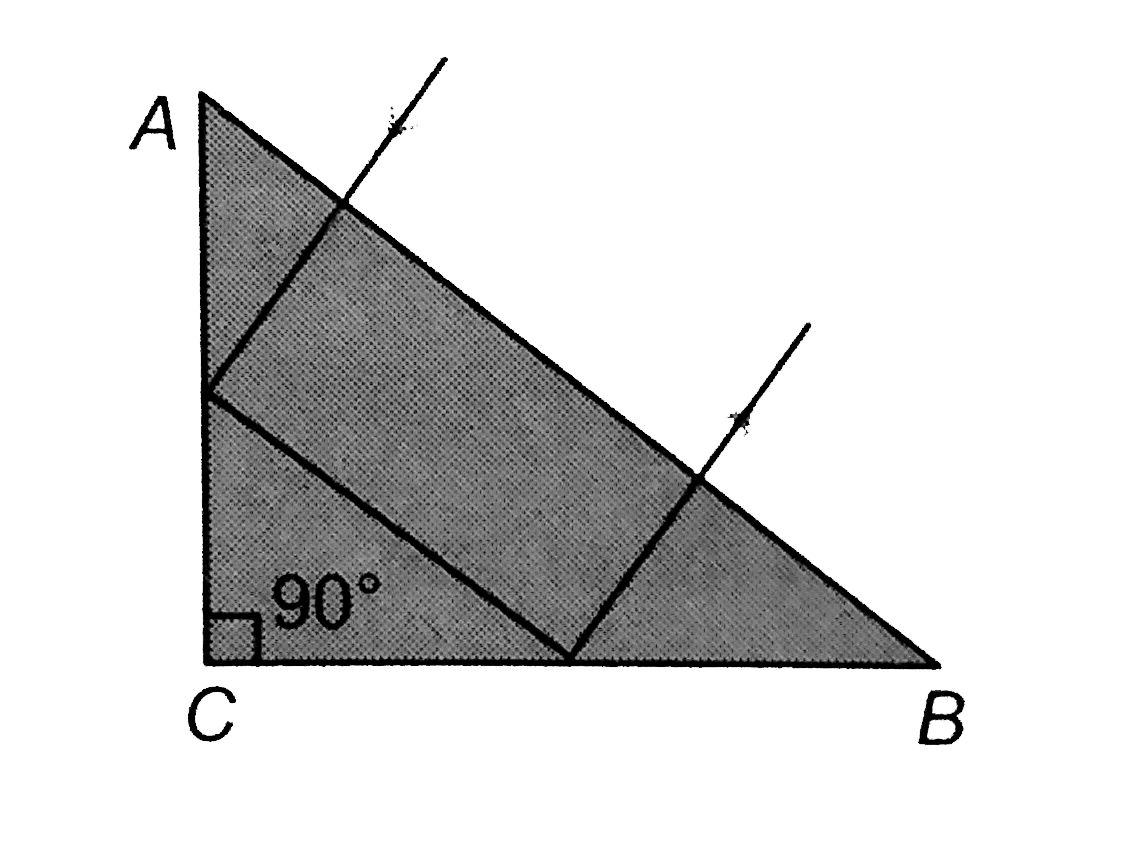 A√2B√3C1.5D2.0
A√2B√3C1.5D2.0
The refractive index of water is 43 and glass is 32. What is the refractive index of glass with respect to water ?
View SolutionA ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be

View SolutionA prism of glass (μ=1.5) is dipped in to water as shown in the figure. If the refractive index of water is 4/3, then the incident ray will be totally reflected if

View Solution
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is 53 and the prism is immersed in water of refractive index 43, then
View Solution
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is 53 and the prism is immersed in water of refractive index 43, then
View Solution
