Question

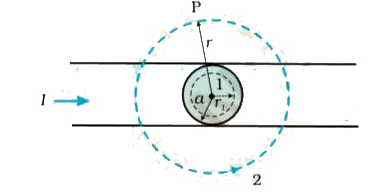
Figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.

Explanation

(a) Consider the case r > a. The Amperian loop, labelled 2, is a circle concentric with the cross-section. For this loop,
`L = 2pi r `
`I_e` = Current enclosed by the loop = I
The result is the familiar expression for a long straight wire
`B(2pi r) = mu_0 I`
`B = (mu_0 I)/(2pi r)`
`B prop 1/r (r gt a)`
(b) Consider the case r < a. The Amperian loop is a circle labelled 1. For this loop, taking the radius of the circle to be r,
`L = 2pi r `
Now the current enclosed Ie is not I, but is less than this value. Since the current distribution is uniform, the current enclosed is,
`I_e = I ( (pi r^2)/(pi a^2)) = (Ir^2)/(a^2)`
Using ampere law `B (2pi r) = mu_0 (Ir^2)/(a^2)`
`B = ((mu_0 I)/(2a^2)) r`
`B prop r " " (r lt a)`

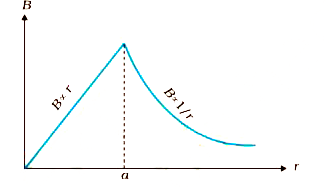
Figure shows a plot of the magnitude of B with distance r from the centre of the wire. The direction of the field is tangential to the respective circular loop (1 or 2) and given by the right-hand rule described earlier in this section. This example possesses the required symmetry so that Ampere’s law can be applied readily.