Two stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s. 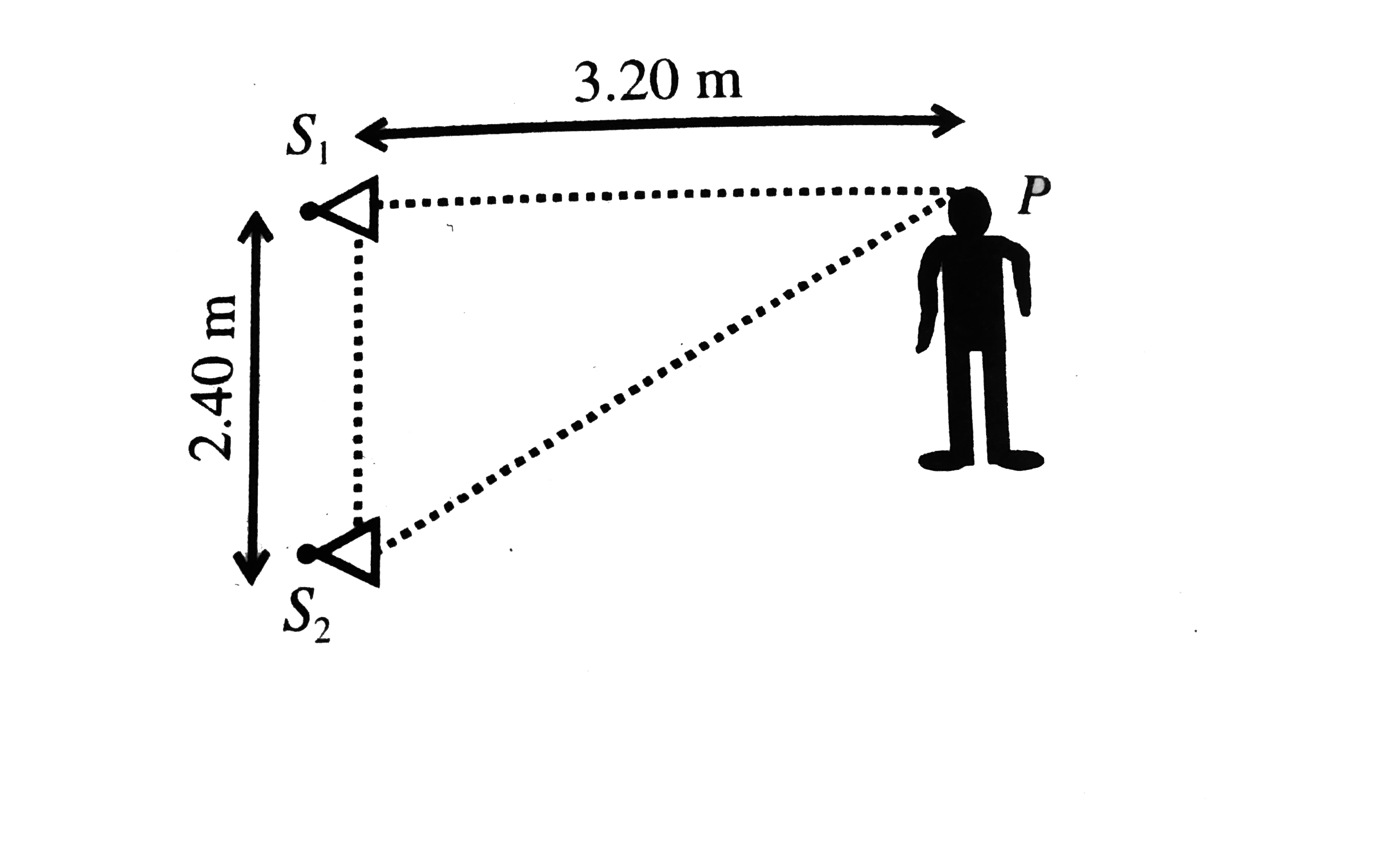
Waves from S1 to S2 reach at point P.
Therefore , the path differnce between waves reaching from S1 to S2 will be Δ=S2P−S1P
Given S1P=3.20m
S2P=√(2.40)2+(3.20)2=4.0m
∴Δ=4.0−3.20=0.80
For minima , path difference
Δ=(2r−1)λ2,r=1,2,3,....
We have λ=v/n , where n is the frequency
Δ=(2r−1)v2n
0.80=(2r−1)v2n
Frequency n=(2r−1)v2×0.80=(2r−1)3201.6Hz=(2r−1)200Hz
Therefore , the required frequencies are n=(2r−1)×200 with r=1,2,....50.
Putting the values of r in the above equation , we get
n=200Hz,600Hz,1000Hz,1400Hz,1800Hz,.....,19800Hz
Similar Questions
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
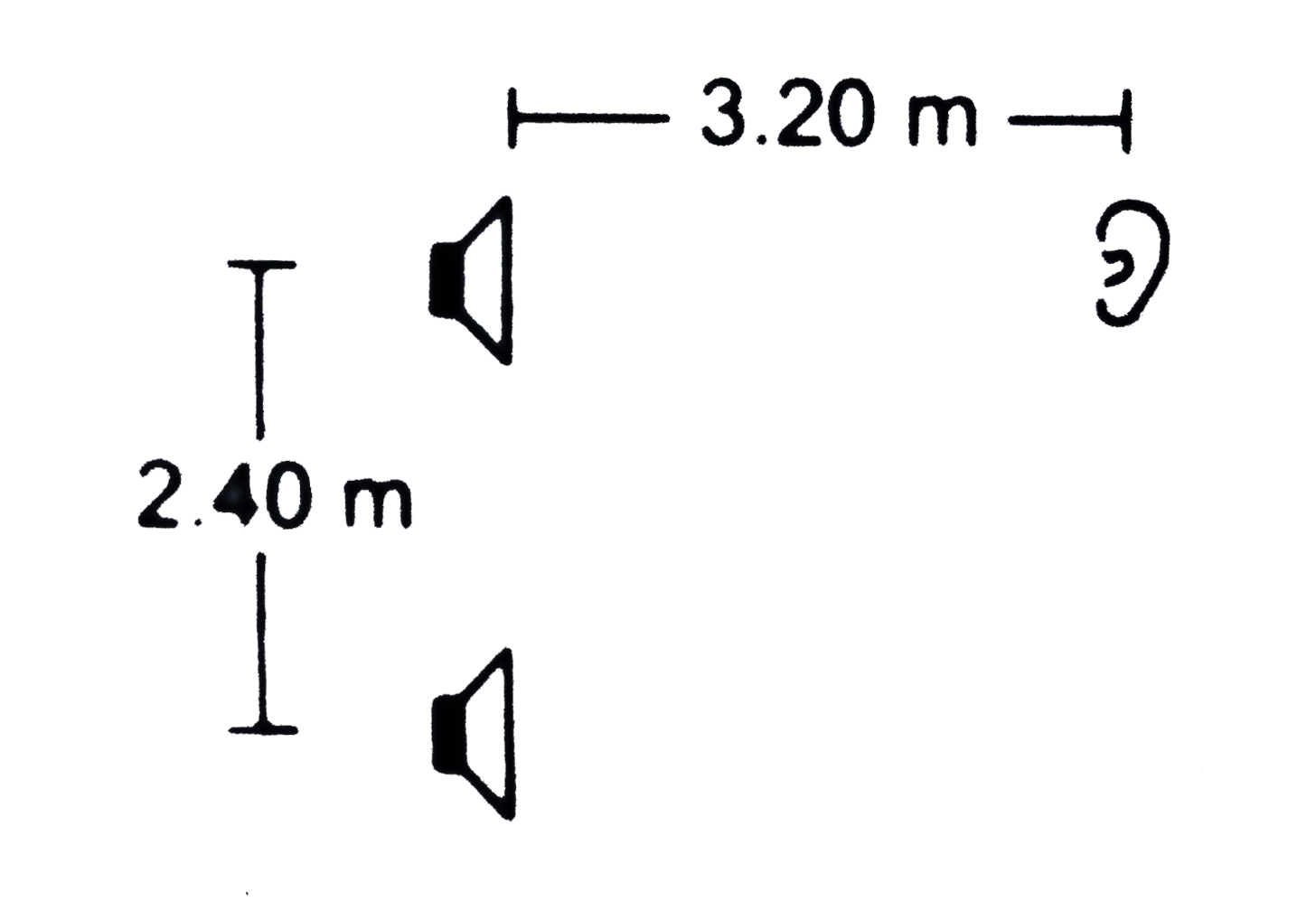
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1

View Solution
Knowledge Check
The minimum distance to hear echo (speed of sound in air is 340m/s)
A15mB16mC17mD18mA source emitting sound of frequency 180Hz is placed in front of a wall at distance of 2m from it . A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air =360m/s.
A3mB2mC3/2mDzero
For human ears, the audible range is 20 Hz to 20,000 Hz.
View SolutionFind the minmimum and maximum wavelengths of sound in water that is in the audible range (20−20000Hz) for an average human ear. Speed of sound in water =1500m/s.
View SolutionTwo sources are placed from a person P as shown in figure. The speed of sound in air is 320m/s.
(a)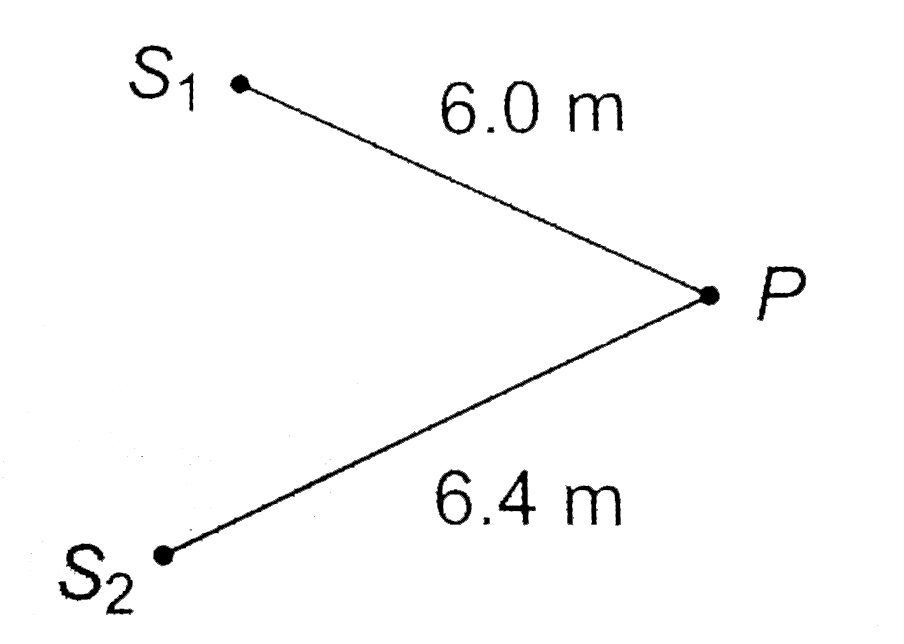
If sound signal is continuously varied from 500Hz to 2500Hz, for which frequency listener will hear minimum sound intensity.
(b)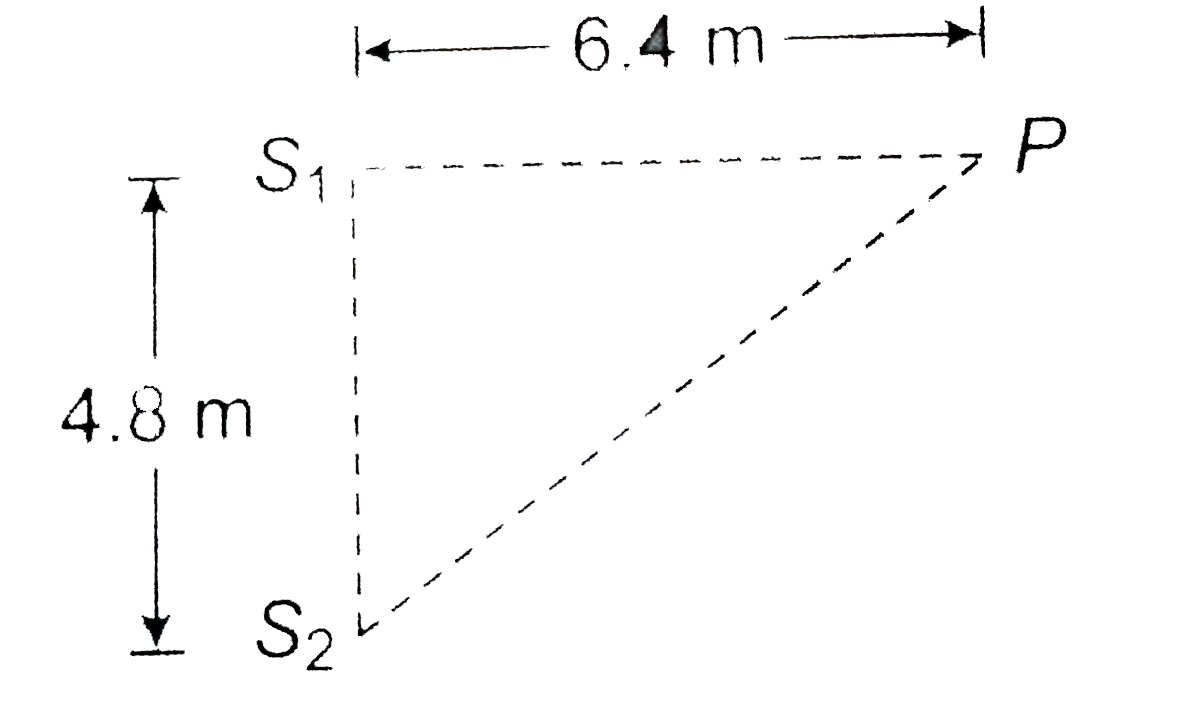
Find the frequencies in audible range (20−20000Hz) for which listener will hear maximum sound intensity.
View SolutionFind the minimum and maximum wavelengths of sound in water that is in the audible range (20-20000 Hz) for an average human ear. Speed of sound in water =1450ms−1.
View SolutionFind the minimum and maximum wavelengths of sound in water that is in the audible range (20-20000 Hz) for an average human ear. Speed of sound in water =1450ms−1.
View SolutionFind the minimum and maximum wavelengths of sound in water that is in the audible range (20-20000 Hz) for an average human ear. Speed of sound in water =1450ms−1.
View Solution
