Two identical loudspeakers placed apart are driven by the same oscillator as shown in Fig. 7.12. A listener is originally at point , located from the centre of the line connecting the two speakers. The listener then moves to point , which is a perpendicular distance from , and she experiences the first minimum sound intensity . What is the frequency of the oscillator ?
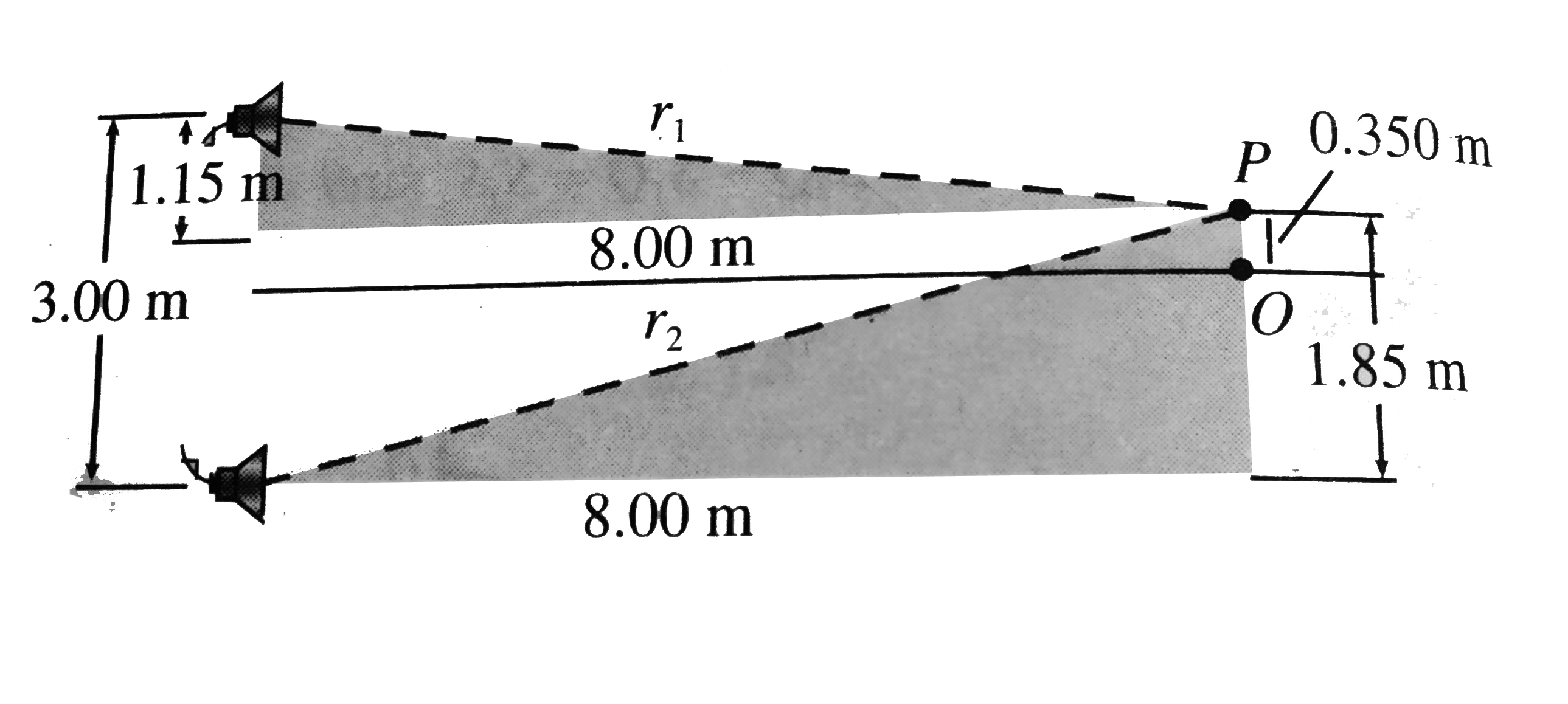
In this example , signal representing the sound is electrically split and sent to two different loudspeakers . After leaving the speakers , the sound waves recombine at the position of the listener. Despite the difference in how the splitting occurs , the path differnce discussion related to Fig . 7.12 can be applied here.
Because the sound waves from two separate sources combine , we apply the waves in interference analysis model. Figure 7.12 shows the physical arrangement of the speakers , along with two shaded right triangles that can be drawn on the basis of the lengths described in the problem . The first minimum occurs when the two waves reaching the listener at point out of phasw , in other words , when their path difference .
From the shaded triangles , find the path lengths from the speakers to the listener :
Hence, the path difference is . Because this path differnce must equal for the first minimum , . To obtain the oscillator frequency , use equation , where is the speed of sound in air , .
Similar Questions
Two loudspeakers are located 3 m apart on the stage of an auditorium. A listener at point P is seated 29.0 m from one speaker and 25.0 m from the other. A signal generator drives the speakers in phase with the same amplitude and frequency. The wave amplitude at P due to each speaker alone is A. The frequency is then varied between 20 Hz and 300 Hz. The speed of sound is 343 m/s.
At what frequency or frequencies will the listener at P hear a maximum intensity?
View SolutionTwo loudspeakers are located 3 m apart on the stage of an auditorium. A listener at point P is seated 29.0 m from one speaker and 25.0 m from the other. A signal generator drives the speakers in phase with the same amplitude and frequency. The wave amplitude at P due to each speaker alone is A. The frequency is then varied between 20 Hz and 300 Hz. The speed of sound is 343 m/s. Determine the value of the maximum amplitude in terms of A.
View SolutionThe two sound amplifiers are located at a distance of 3m from each other as shown in the picture below and are in the same art. Assuming that the amplitude of the sounds emanating from the speakers is approximately the same at the position of the listener, which is 4.0 m away in front of one of the speakers. Determine for which frequencies the listener will hear the minimum signal. The speed of sound in air is 330 m / s.
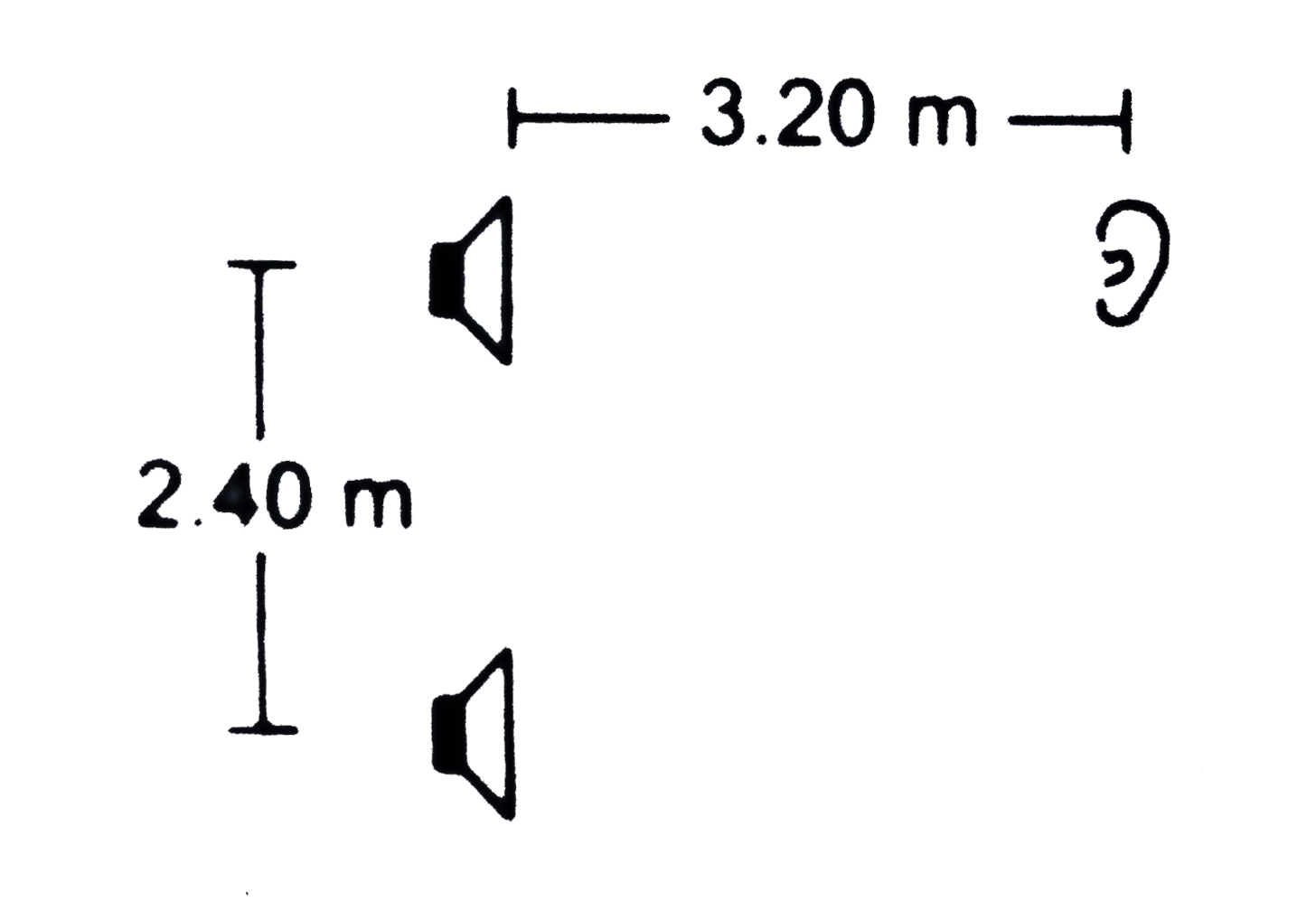
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
View SolutionTwo sound speakers are driver in phase by an audio amplifier at frequency 600 H_(Z) . The speed of sound is 340 m//s . The speakers are on the y - axis, one at y = + 1.0 m and the other at y = - 1.0 m . A listener begins at y = 0 and walks along a line parallel to the y - axis at a very large distance x away. (a) At what angle theta (between the line from the origin to the listener at the x - axis) will she first hear a minimum sound intensity? (b) At what angle will she first hear a maximum (afer theta = o^(@) ) sound intensity? (c ) How many maxima can she possible hear if she keeps walking in the same direction?
View SolutionTwo identical speakers emit sound waves of frequency 680HZ uniformly in all directions with a total audio output of 1mW each. The speed of sound in air is 340m/s. A point P is a distance 2.00m from one speaker and 3.00m from the other.
(a) Finf the intensity I1 and I2 from rach speaker at point p separately.
(b) If the speakers are driven coherently and in phase, what is the intensity at point p?
(c ) If they driven coherently but of phase by 180∘, what is the intensity at point P?
(d) If the speakers are incoherent, what is the intensity at point p?
View SolutionThe distance between the two identical speakers shown in Fig. 14.3.3 are 4.00m. They are driven by the same osicllator. Initially a listner stays at L at a distance 8.0 m from the centre of the line connecting the two speakers. The listner then walks to the point A where AL=0.4m. The first minium is sound intensity in heard just the listener reaches the point A. Find the frequency of the oscillator. Speed of sound in air is 340 m/s.
View SolutionAn oscillator of frequency 680Hz drives two speakers . The speakers are fixed on a vertical pole at a distance 3m from each other as shown in Fig. 7.103. A person whose height is almost the same as that of the lower speaker walks towards the lower speaker in a direction perpendicular to the pole. Assuming that there is no reflection of sound from the ground and speed of sound is v=340m/s , answer the following questions.

As the person walks towards the pole , his distance from the pole when he first hears a minimum in sound intensity is nearly
View Solution
