One end of a horizontal string is attached to a vibrating blade , and the other end passes over a pulley as in Fig. 7.49 (a). A sphere of mass $2.00 k g$ hangs at the end of the string . The string is vibrating in its second harmonic . A container of water is raised under the sphere so that the sphere is completely submerged . In this configuration , the string vibrates in its fifth harmonic as shown in Fig . 7.49 (b). What is the radius of the sphere ?

Text Solution

Verified by Experts

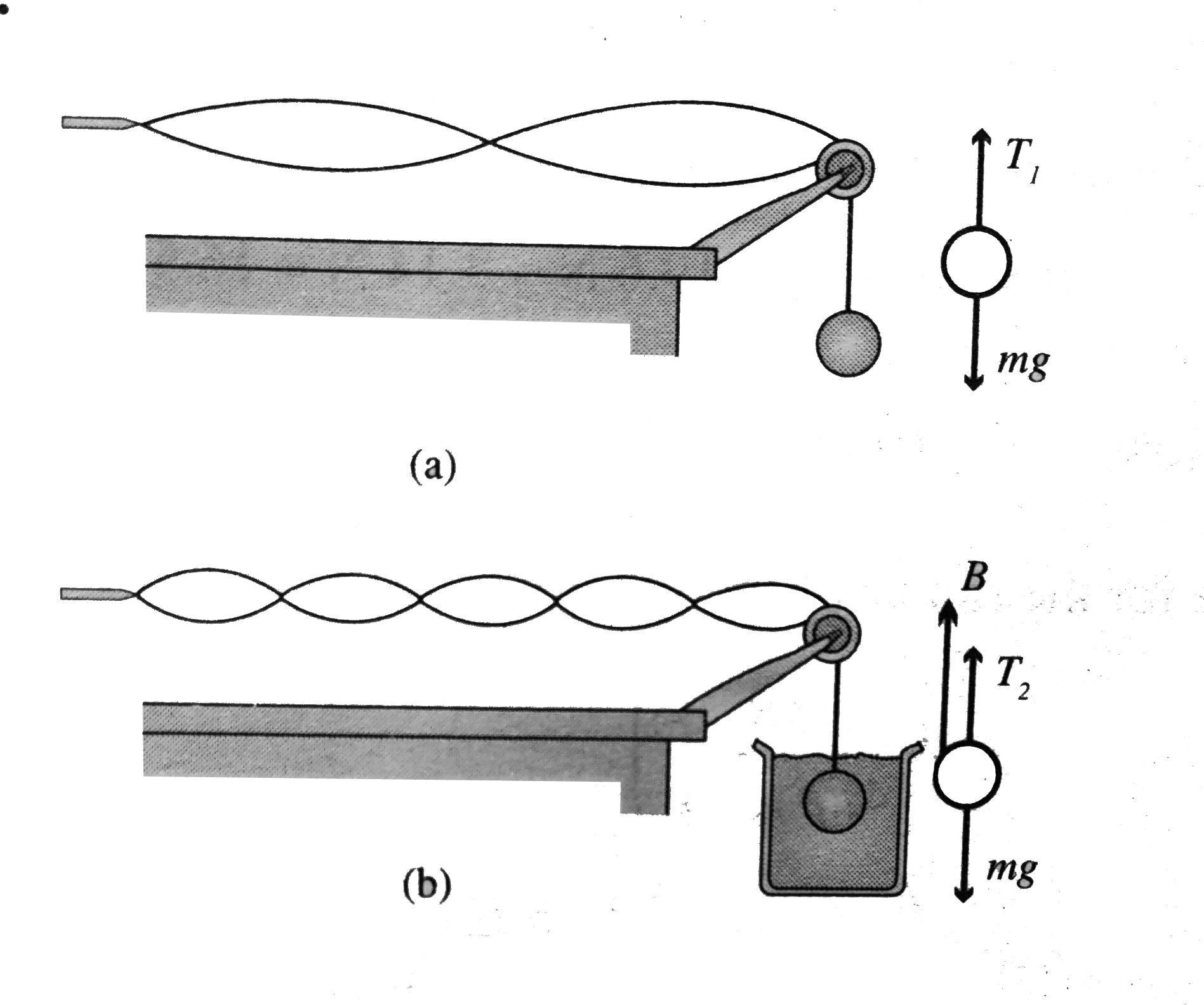
Imagine what happens when the sphere is immersed in the water . The buoyant force acts upward on the sphere , reducing the tension in the string . The change in tension causes a change in the speed of waves on the string , which in turn causes a change in the wavelength . This altered wavelength results in the string vibrating in its normal mode rather than the second .
The hanging sphere is modelled as a particle in equilibrium . One of the forces acting on it is the buoyant force from the water . we also apply the waves under boundary conditions model to the string .
Apply the particle in equilibrium model to the sphere in Fig . 7.49 (a) , identifying $T_{1}$ as the tension in the string as the sphere hangs in air .
$T_{1} = m g$ (i)
Apply the particle in equilibrium model to the sphere in Fig . 7.49 (b) , where $T_{2}$ is the tension in the string as the sphere is immersed in water . ltbr> $B + T_{2} = m g \Rightarrow B = m g - T_{2}$ (ii)
The desired quantity , the radius of the sphere , will appear in the expression for the buoyant force $B$ . Before proceeding in this direction , however , we must evalute $T_{2}$ from the information about the standing wave .
Write the equation for the frequency of a standing wave on a string twice , once before the sphere is immersed and once after . Notice that the frequency $f$ is same in both the cases because it is determined by the vibrating blade . In addition , the linear mass density $μ$ and the length $L$ of the vibrating portion of the string are same in both cases . Divide the two equations.
$f = \frac{n_{1}}{2 L} \sqrt{\frac{T_{1}}{μ}}$ (iii)
$f = \frac{n_{2}}{2 L} \sqrt{\frac{T_{2}}{μ}}$ (iv)
$1 = \frac{n_{1}}{n_{2}} \sqrt{\frac{T_{1}}{T_{2}}}$ (v)
solve for $T_{2}$ :
$T_{2} = {(\frac{n_{1}}{n_{2}})}^{2} T_{1} = {(\frac{2}{5})}^{2} (19.6 N) = 3.14 N$
Substituting this result into Eq. (ii)
$B = m g - T_{2} = 19.6 N - 3.14 N = 16.5 N$
Now $B = ρ_{w a t e r} g V_{s p h e r e} = ρ_{w a t e r} g (\frac{4}{3} π r^{3})$
Solve for the radius of the sphere :
$r = {(\frac{3 B}{4 π ρ_{w a t e r} g})}^{1 / 3}$
$= \frac{3 (16.5 N)}{{(4 π (1000 k g / m^{3}) (9.80 m / s^{2}))}^{1 / 3}}$
$= 7.38 \times 10^{- 2} m = 7.38 c m$
Notice that only certain radii of the sphere will result in the string vibrating in a normal mode , the speed of waves on the string must be changed to a value such that the length of the string is integer multiple of half wavelengths . The radii of the sphere that cause the string to vibrate in a normal mode are quantized.

Updated on:21/07/2023

If a string fixed at both ends, vibrates in its fourth harmonic, the wavelength is 15 cm. What is the length of the string ?
A20 c m
B30cm
C25 cm
D40 cm
A stretched string is vibrating in the second overtone, then the number of nodes and anti-nodes between the ends of the string are respectivley
A3 and 4
B4 and 3
C2 and 3
D3 and 2
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is $:$
A $\frac{g}{2}$
B $\frac{g}{3}$
C $\frac{g}{5}$
D $\frac{g}{10}$