Question

(a) what are coherent sources of light ? Two slits in Young's double slit experiments are illuminated by two different sodium lamps emitting light of the same wavelength. Why is no interference pattern observed?
(b) Obtain the condition for getting dark and bright fringes in Young's experiment. Hence write the expression for the fringe width.
(c) If s is the size of the source and its distance from the plane of the two slits, what should be the criterion for the interference fringes to be seen ?

Explanation

(a) Coherent sources of light : The sources of light, which emit continuous light waves of the same wavelength, same frequency and in same phase are called coherent sources of light.
Interference pattern is not obtained. This is because phase difference between the light waves emitted from two different sodium lamps will change continuously.
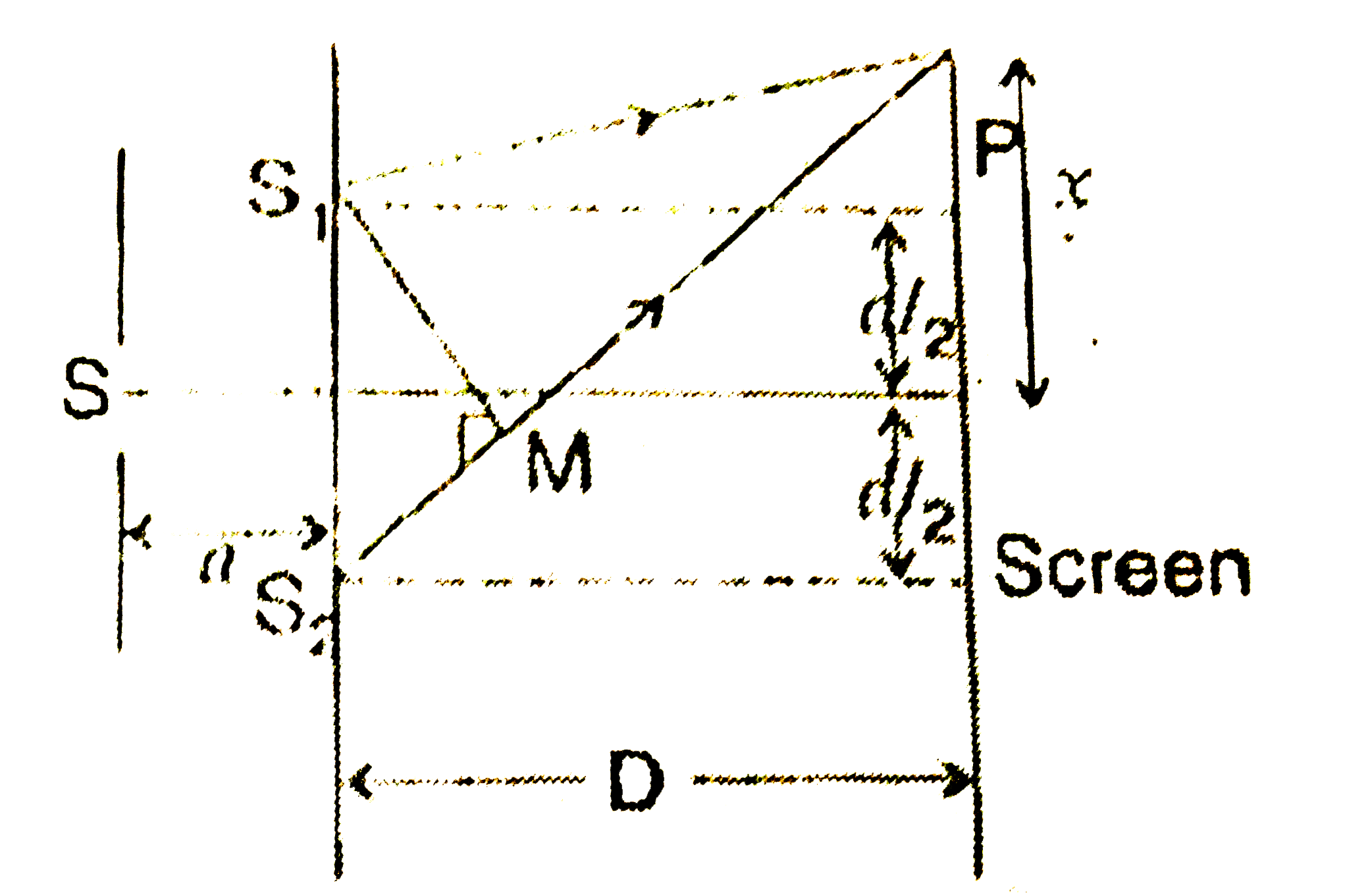
(b) For bright fringes (maxima),
Path difference, `(xd)/(D) = n lambda`
`x=n lambda(D)/(d) `, where n=0, 1, 2, 3, ......
For dark fringes (minima),
Path difference, `(xd)/(D)=(2n-1) (lambda)/(2) :. x=(2n-1) (lambda)/(2) (D)/(d)`, where n=0, 1, 2, 3, ...
The separation between the centre of two consecutive bright fringes is the width of a dark fringe.
`:.` Fringe width `P=x_(n)-x_(n-1)`
`beta=n(lambdaD)/(d) - (n-1) (lambdaD )/(d) :. beta = (lambda D)/(d)`
(c) The condition for interference fringes to be is `(d phi)/(dt)=-(d)/(dt)`.
For interference fringes to be seen, the condition `(S)/(a) lt (lambda)/(d)` should be satisfied.