A metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.

Video Solution

Text Solution

Verified by Experts

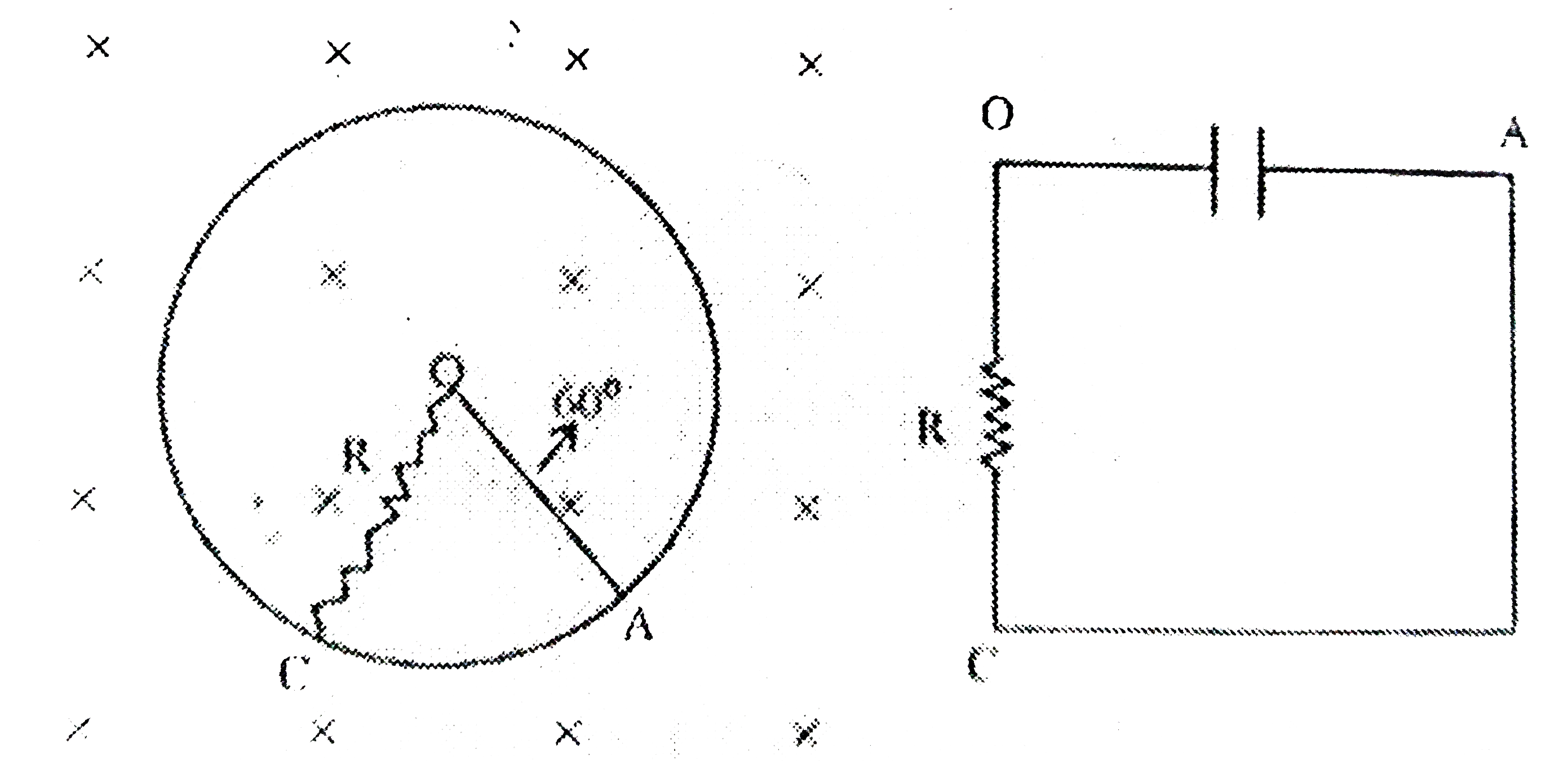
In time t, if $θ$ is angle traced by face end then area swept $A = π l^{2} \times (\frac{θ}{2 π}) = \frac{1}{2} l^{2} θ$
$ϕ = B A {cos 0}^{\circ} = \frac{1}{2} B l^{2} θ$
$\frac{d ϕ}{d t} = \frac{1}{2} B l^{2} (\frac{d ϕ}{d t}) = \frac{1}{2} B l^{2} ω$
The positive charge of the rod will be pushed towards O be replaced by a battery of emf source $\frac{1}{2} B ω l^{2}$ with the positive terminal towards O. The equivalent circuit diagram is shown in figure. The circular loop joins A to C by a resistance less path. The current in the resistance R is
$i = \frac{\in}{R} = \frac{B ω I^{2}}{2 R}$

Updated on:21/07/2023