Question

Use Huygens's principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band ?

Explanation

Let AB be a slit of width 'a' and a parallel beam of monochromatic light is incident on it. According to Huygen's principle the diffraction pattern is the result of superposition of a large number of waves, starting from different points of illuminated slit.

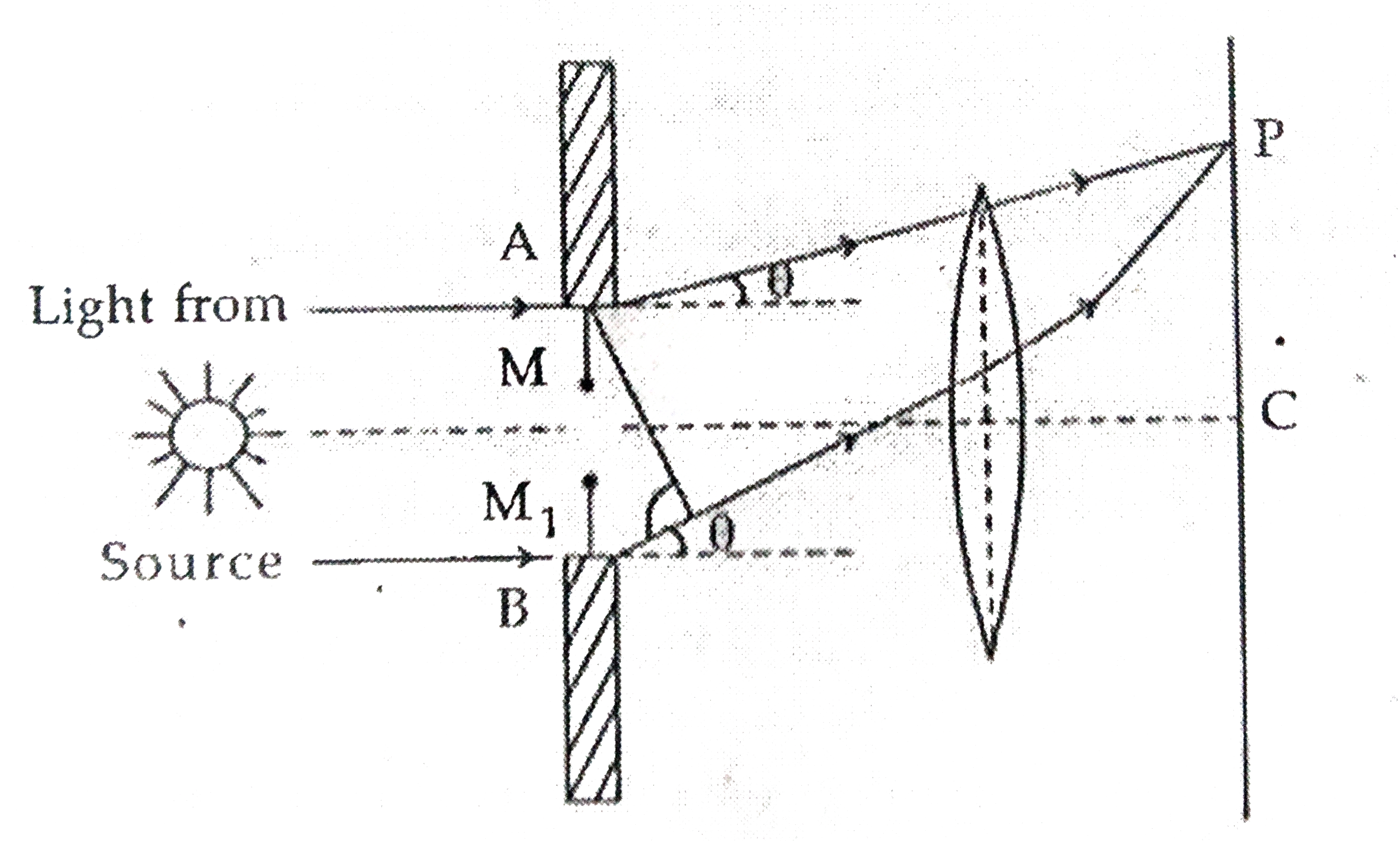
At the central point C of the screen, the angle `theta` is zero. Hence the waves starting from all points of slit arrive in the same phase. This gives maximum intensity at the central point C.
The observation point in now taken at P.
Minima : Now we divide the slit into two equal halves AO and OB, each of width `(a)/(2)`. Now for every point, `M_(1)` in AO, there is a corresponding point `M_(2)` in OB, such that `M_(1) M_(2)=(a)/(2)`, Then path difference between waves arriving at P and starting from `M_(1) " and " M_(2)` will be
`(a)/(2) sin theta =(lamda)/(2)`
`a sin theta = lamda`
In general, `a sin theta = n lamda`
Secondary Maxima : Similarly, it can be shown that for maxima
`a sin theta =(n+(1)/(2))lamda`
The intensity pattern on the screen is shown in the given figure.

When the width of the slit is made double the original width, the size reduces by half according to the relation : size `- lamda // d`. Intensity increases four fold.