(a) In Young's double slit experiment, derive the condition for (i) constructive interference and (ii) destructive interference at a point on the screen.
(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference frings in a Young's double slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.

Video Solution

Text Solution

Verified by Experts

(a) Young's double slit experiment : Consider two narrow rectangular slits $S_{1} and S_{2}$ placed perpendicular to the plane of paper. Slit S is placed on the perpendicular bisector on $S_{1} S_{2}$ and illuminated with monochromatic light.
The slits are separated by a small distance d. A screen is placed at a distance D from $S_{1}, S_{2} .$ Consider a point P on the screen at distance x from O. The path difference between the waves reaching P from $S_{1} and S_{2}$ is :
$P = S_{2} P - S_{1} P$
Draw $S_{1} N$ perpendicular to $S_{2} P .$ Then,
$P = S_{2} P - S_{1} P = S_{2} P - N P = S_{2} N$
From right-angled $Δ S_{1} S_{2} N, \frac{S_{2} N}{S_{2} S_{1}} = sin θ$
$P = S_{2} N = S_{2} S_{1} sin θ = d sin θ$

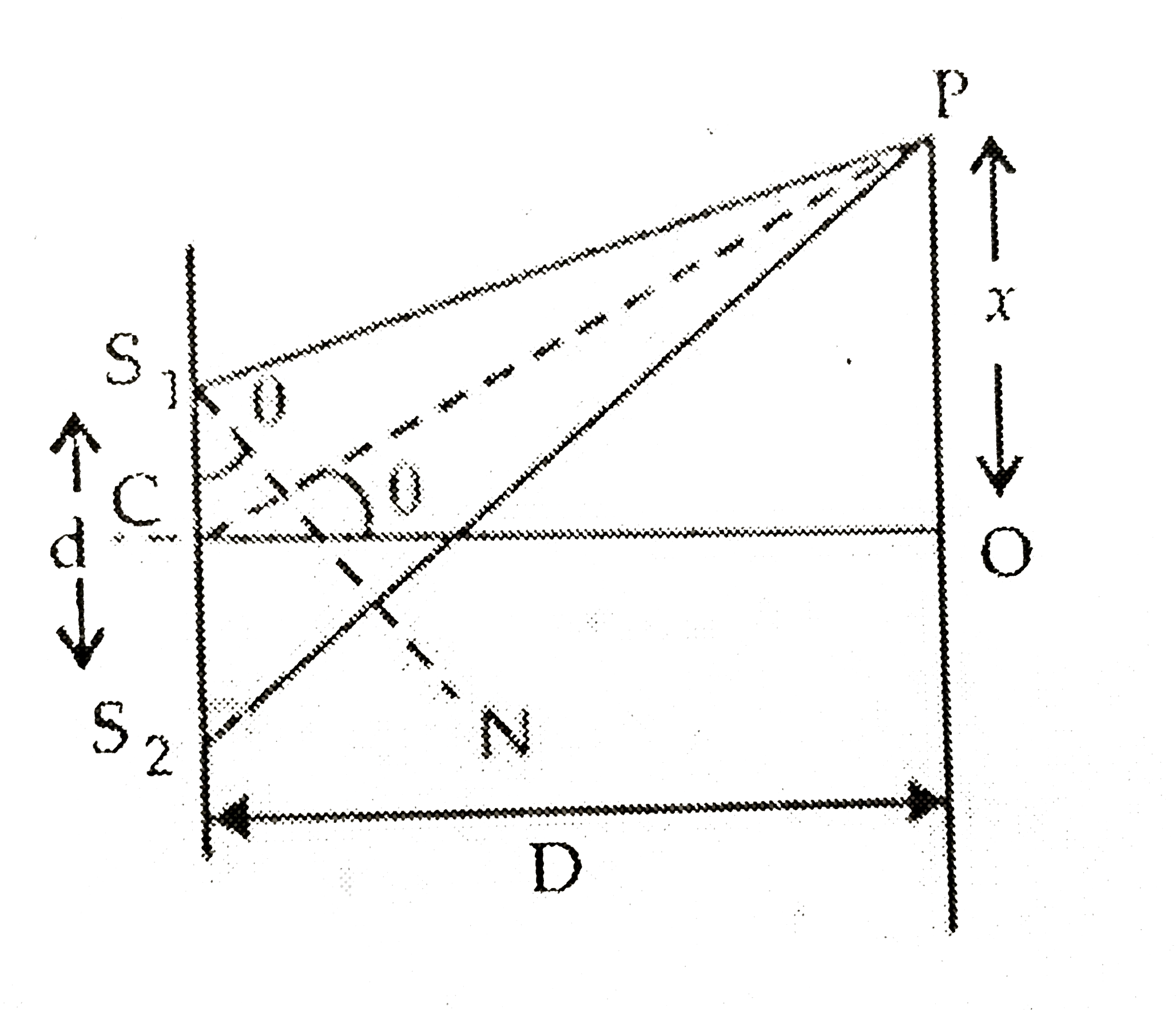
From $Δ C O P, when θ$ is small
$sin θ \approx θ \approx tan θ = \frac{x}{D} ∴ P = \frac{x d}{D}$
For constructive interference,
$\frac{x d}{D} = n λ, n = 0, 1, 2, 3, ... .$
When n=0 $x_{n} = 0,$ central bright is formed at O.
For destructive interference,
$\frac{x d}{D} = (2 n + 1) \frac{λ}{2} or x_{n} = (2 n + 1) \frac{λ D}{2 D} = \frac{1}{2} \frac{λ D}{d}, \frac{3}{2} \frac{λ D}{d}, \frac{5}{2} \frac{λ D}{d}, ...$
Thus, alternate bright and dark fringers are formed on the screen.
(b) Given
$\begin{matrix} λ_{1} = 800 n m = 800 \times 10^{- 9} m λ_{1} = 800 n m = 800 \times 10^{- 9} m λ_{2} = 600 n m = 600 \times 10^{- 9} m \end{matrix}$
D=1.4m
$d = 0.28 m m = 0.28 \times 10^{- 3} m$
Let $n_{1}^{t h}$ maximum corresponds to $λ_{1}$ coincides with $n_{2}^{t h}$ maximum corresponds $λ_{2} .$ Then
$n_{1} \frac{λ_{1} D}{d} = n_{2} \frac{λ_{2} D}{d} or, \frac{n_{1}}{n_{2}} = \frac{n_{2}}{n_{1}} = \frac{600}{800} = \frac{3}{4}$
The minimum integral value of $n_{1}$ is 3 and of $n_{2}$ is 4. Therefore, the minimum value of y is
$y mix = \frac{λ_{1} D}{d} = \frac{3 \times 800 \times 10^{- 9} \times 1.4}{0.28 \times 10^{- 3}} \Rightarrow y mix = 12 m m$
Position of first bright fringe.
$λ_{A} = 800 n m = 800 \times 10^{- 9} m = 8 \times 10^{- 7} m .$
$X_{A} = λ \frac{D}{d}$
$= 8 \times 10^{- 7}$
$d = 0.28 m m, = 0.28 \times 10^{- 3} m .$
$D = 1.4 m$ .
$X_{A} = λ \frac{D}{d} = \frac{8 \times 10^{- 7} \times 1.4}{0.28 \times 10^{- 3}} = 4 \times 10^{- 4} \times 10 = 4 \times 10^{- 3} M .$
$For wavelength λ_{B} = 600 n m = 600 \times 10^{- 9} m .$
$6 \times 10^{- 7}$ M. Position of first bright fringe is
$X_{B} = λ \frac{D}{d} = \frac{6 \times 10^{- 7} \times 1.4}{0.28 \times 10^{- 3}} = 3 \times 10^{- 7} \times 10^{- 3} \times 10 = 3 \times 10^{- 3} m .$
The least distance from the central maximum, where the bright fringes coincides.
$= X_{A} - X_{B} = 4 \times 10^{- 3} - 3 \times 10^{- 3} = 1 \times 10^{- 3} m = 1 n m .$

Updated on:21/07/2023

Interference fringes in Young's double slit experiment with monochromatic light are
Aalways equispaced
Balways unequally spaced
Cboth equally and unequally spaced
Dformed by a portion of the wave front.
In Young's double slit experiment, if one of the slit is closed fully, then in the interference pattern
A(a) A bright slit will be observed, no interference pattern will exist
B(b) The bright fringes will become brighter
C(c) The bright fringes will become fainter
D(d) None of the above
In Young's double slit experiment, the interference bright fringes are of:
Aequal widths and unequal intensities
Bunequal width and equal intensities
Cequal widths and equal intensities
Dunequals widths and unequal intensities