Question

(a) How is a toroid different from a solenoid?
(b) Show that in an ideal toroid, the magnetic field (i) inside the toroid and (ii) outside the toroid at any point in the open space is zero.

Explanation

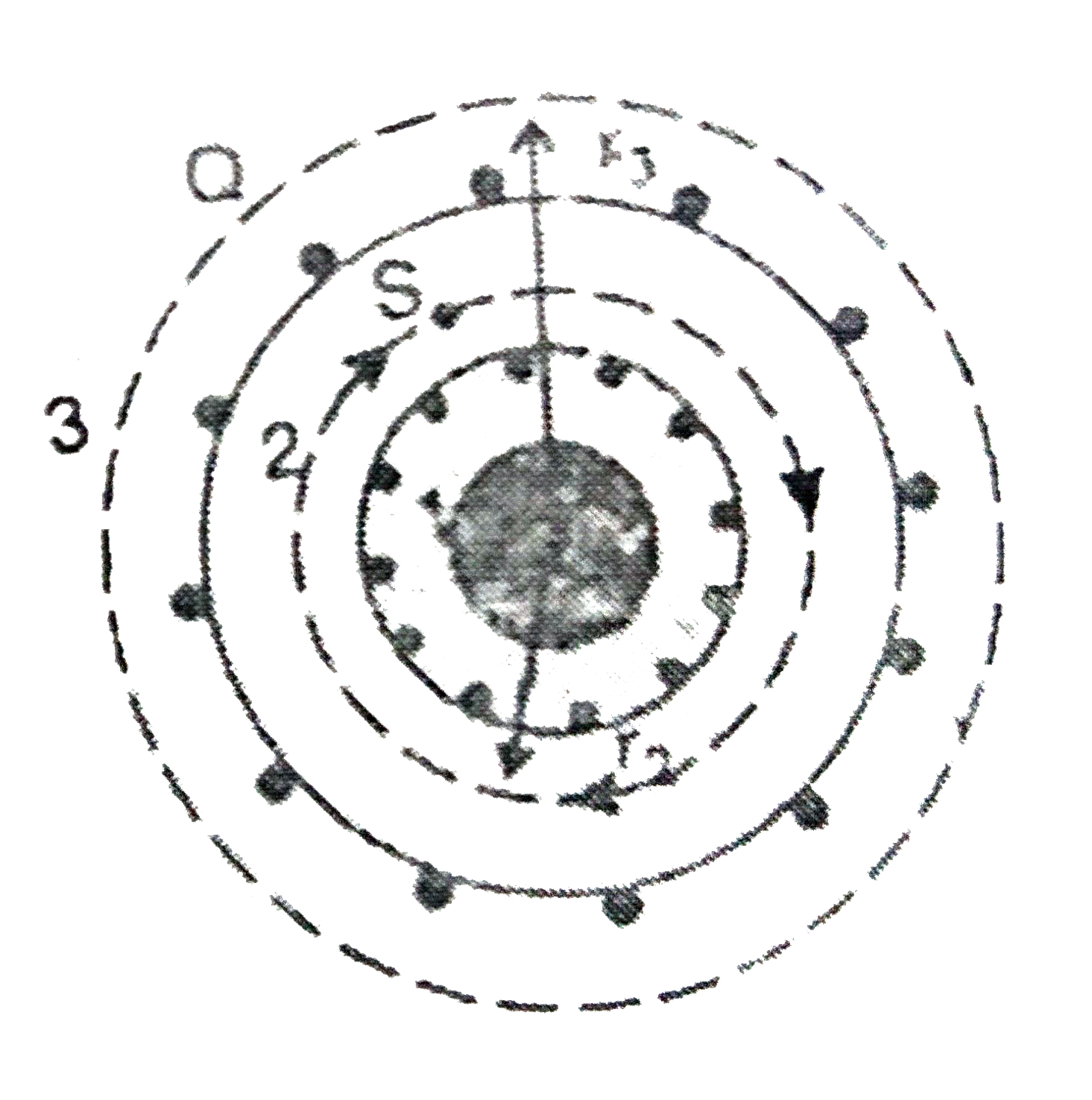
A toroid is essentially a solenoid which has been bent into a circular shape to close on itself.
(b) For the loop 1, Ampere's circuital law gives
`B_(1).2pi r_(1)=mu_(0)(0)" i.e. "B_(1)=0`
Thus, the magnetic field, in the open space inside the toroid is zero.
Also at point Q we have `B_(3)(2pi r_(3))=mu_(0)(I("enclosed"))`
But from the sectional cut, we see that the current coming out the plane of the paper is cancelled exactly by the current going into it.
Hence `I_("enclosed")=0" "thereforeB_(3)=0`