Question

A convex lens of focal length 20cm is placed coaxilly with a convex mirror of radius of curvature 20 cm. The two are kept 15 cm apart. A point object is placed 40 cm in front of the convex lens. Find the position of the image formed by this combination. Draw the ray diagram showing the image formation.

Explanation

Let us first locate the image of the point obect S formed by the convex lens.
Here:
`u=-40cm,and,f=20cm`
From the lens formula, we have:
`(1)/(v)-(1)/(u)=(1)/(f)rArr(1)/(v)=(1)/(u)+(1)/(f)`
`(1)/(20)+(1)/(-40)=v=40cm`

The positive sign shows that the image is formed to the right of the lens as shown in the following figure.
The image `I_(1)` is formed behind the mirror and hence acts as a virtual source for the mirror. The convex mirror forms the image `L_(2)`, whose distance form the mirror can be calcualted as :
`(1)/(v)+(1)/(u)=(1)/(f)`
Hence : `u=25cm and, f=R//2=10cm`
`(1)/(v)=(1)/(f)-(1)/(u)rArr(1)/(v)=(1)/(10)-(1)/(25)`

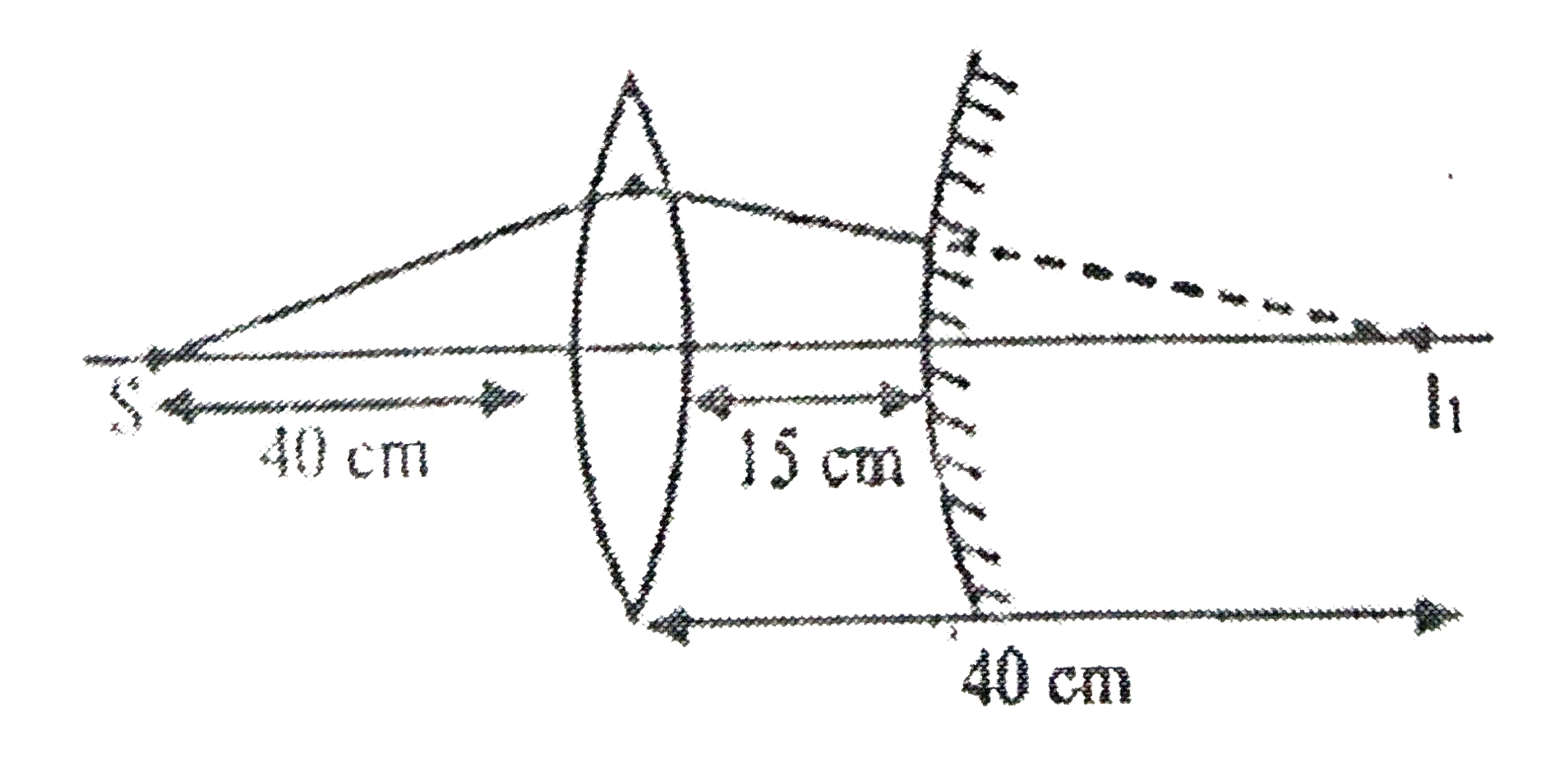
Hence, the final image is formed at a distance of 16.67 cm from the convex mirror as shown in the following figyure.