The figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
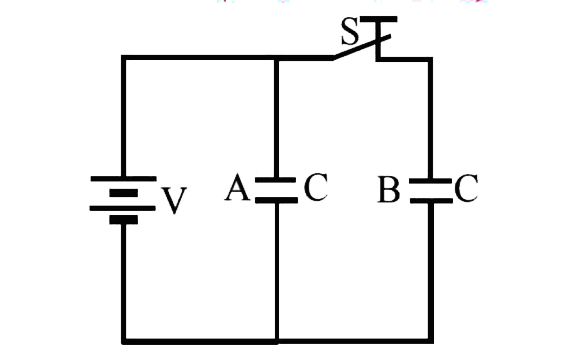
Let C is the capacitance of both the capacitor .
(i) Initially, when switch S is closed
Net capacitance
Total initial energy =
After filling the gap ,
(ii) When switch is open, the capacitance in each of the capacitions varies, hence , the energy
also varies i.e., in case of 'B' , the change remains same,.i.e., CV and the capacity of each
capacitor becomes potenial of conneted, capacitor, remains same so CV
= KCV' here is potential of disconnected capacitor
Ratio .
Topper's Solved these Questions
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-C55videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]12videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-A31videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
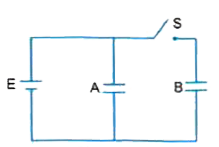
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed . The switch is now opened and the free space between the plates of the capacitors is filled with dielectric of dielectric constant K . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric .
 View Solution
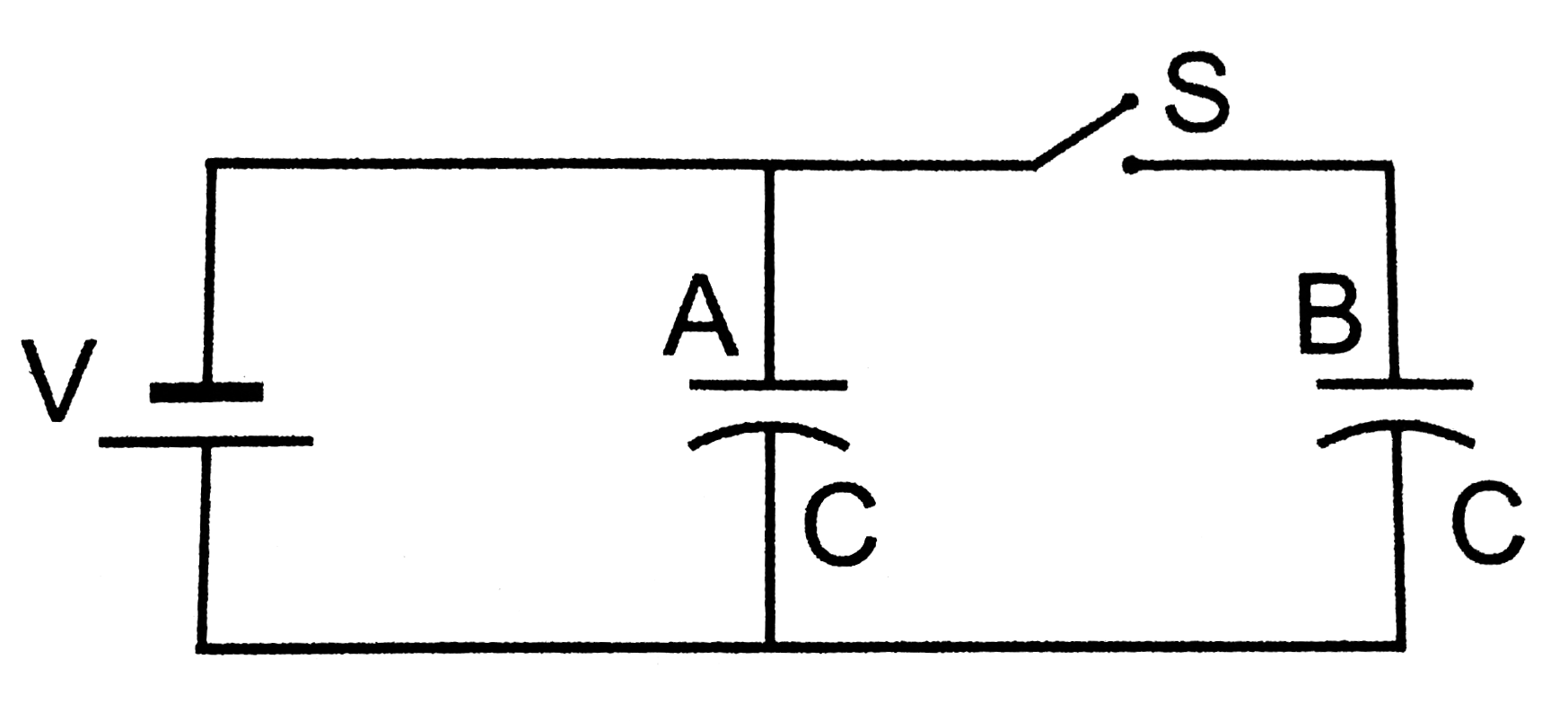
View SolutionFigure shows two indentical pallel plate capacitors connected to a switch S. Initially ,the switch is closed so that the capacitors are completely charged .The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical air filled parallel plate capacitors are charged to the same potential in the manner shown by closing the switch S. If now the switch S is opened and the space between the plates is filled with a dielectric of relative permittivity εt, then
 Athe potential difference as well as charge on each capacitor goes up by a factor εrBthe potential difference as well as the charge on each capacitor goes down by a factor εrCthe potential difference across A remains constant and the charge on B remains unchangedDthe potential difference across B remains constant, while the charge on A remains unchanged
Athe potential difference as well as charge on each capacitor goes up by a factor εrBthe potential difference as well as the charge on each capacitor goes down by a factor εrCthe potential difference across A remains constant and the charge on B remains unchangedDthe potential difference across B remains constant, while the charge on A remains unchanged - Question 2 - Select One
Two identical air filled parallel plate capacitors are changed to the same potential in the manner shown by closing the switch S. If now the switch S is opened and the space between the plates is filled with a dielectric of relative permittivity εr, then
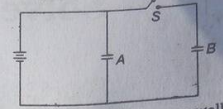 Athe potential difference as well as charge on each capacitor goes up by a factor εrBthe potential difference as well as charge on each capacitor goes down by a factor εrCthe potential difference across A remains constant and the charge on B remains unchangedDthe potential difference across B remains constant and the charge on A remains unchanged
Athe potential difference as well as charge on each capacitor goes up by a factor εrBthe potential difference as well as charge on each capacitor goes down by a factor εrCthe potential difference across A remains constant and the charge on B remains unchangedDthe potential difference across B remains constant and the charge on A remains unchanged - Question 3 - Select One
Two identical air filled parallel plate capacitors are changed to the same potential in the manner shown by closing the switch S. If now the switch S is opened and the space between the plates is filled with a dielectric of relative permittivity εr, then
 Athe potential difference as well as charge on each capacitor goes up by a factor εrBthe potential difference as well as charge on each capacitor goes down by a factor εrCthe potential difference across A remains constant and the charge on B remains unchangedDthe potential difference across B remains constant and the charge on A remains unchanged
Athe potential difference as well as charge on each capacitor goes up by a factor εrBthe potential difference as well as charge on each capacitor goes down by a factor εrCthe potential difference across A remains constant and the charge on B remains unchangedDthe potential difference across B remains constant and the charge on A remains unchanged
A parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionIf the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionWhen a dielectric is inserted in the space between parallel plates of a charged capacitor, then
View Solution

