Plot a graph showing variation of a de Broglie wavelength (λ) associated with a charged particle of mass m, verses 1/√V, where V is the potential difference thrugh which the particle is accelerated. How does this graph give us the information the magnitude the magnitude of the charge of the particle ?
To solve the problem of plotting the graph showing the variation of de Broglie wavelength (λ) associated with a charged particle of mass m versus 1√V, we will follow these steps:
1. Understand de Broglie Wavelength:
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
2. Relate Momentum to Kinetic Energy:
For a charged particle accelerated through a potential difference V, the kinetic energy (KE) gained by the particle is given by:
KE=QV
where Q is the charge of the particle.
3. Express Momentum in Terms of Kinetic Energy:
The momentum p can be expressed in terms of kinetic energy as:
p=√2m⋅KE=√2m⋅QV
4. Substitute Momentum into de Broglie Wavelength Formula:
Substituting the expression for momentum into the de Broglie wavelength formula, we get:
λ=h√2m⋅QV
5. Rearranging the Equation:
Rearranging the equation gives us:
λ=h√2mQ⋅1√V
This shows that λ is inversely proportional to √V.
6. Plotting the Graph:
- On the x-axis, plot 1√V.
- On the y-axis, plot λ.
- The relationship indicates that as 1√V increases, λ decreases, resulting in a straight line graph that passes through the origin.
7. Slope of the Graph:
The slope of the graph can be expressed as:
slope=h√2mQ
This means that the slope is directly related to the charge Q of the particle.
8. Determining the Charge:
From the slope, if we know the values of h (Planck's constant) and m (mass of the particle), we can rearrange the slope equation to find the charge Q:
Q=h22m⋅slope2
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
For a charged particle accelerated through a potential difference V, the kinetic energy (KE) gained by the particle is given by:
KE=QV
where Q is the charge of the particle.
The momentum p can be expressed in terms of kinetic energy as:
p=√2m⋅KE=√2m⋅QV
Substituting the expression for momentum into the de Broglie wavelength formula, we get:
λ=h√2m⋅QV
Rearranging the equation gives us:
λ=h√2mQ⋅1√V
This shows that λ is inversely proportional to √V.
- On the x-axis, plot 1√V.
- On the y-axis, plot λ.
- The relationship indicates that as 1√V increases, λ decreases, resulting in a straight line graph that passes through the origin.
The slope of the graph can be expressed as:
slope=h√2mQ
This means that the slope is directly related to the charge Q of the particle.
From the slope, if we know the values of h (Planck's constant) and m (mass of the particle), we can rearrange the slope equation to find the charge Q:
Q=h22m⋅slope2
Topper's Solved these Questions
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-C55videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]12videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-A31videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Write the relationship of de-Broglie wavelength λ associated with a particle of mass m in terms of its kinetic energy.
View SolutionWrite the expression for the de-Broglie wavelength associated with a charge particle having charge 'q' and mass 'm', when it is accelerated by a potential V.
View Solution
Knowledge Check
- Question 1 - Select One
The de-Broglie wavelength λ associated with charged particle of charge q, mass m and potential difference V is
Ah√2mqVBh2√2mqVCh√mqVDh√2qV - Question 2 - Select One
The de - Broglie wavelength associated with the particle of mass m moving with velocity v is
Ah/mvBmv/hCh/2vDm/hv - Question 3 - Select One
The graph showing the relation between de Broglie wavelength λ of particle and its temperature T is
A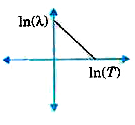 B
B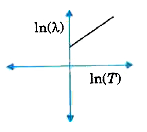 C
C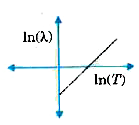 D
D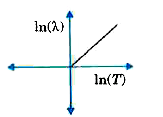
Write the expression for the de-Broglie wavelength associated with a charged particle having charge 'q' and mass 'm' when it is accelerated by a potential V.
View SolutionThe wavelength of a charged particle ………….. the square root of the potential difference through which it is accelerated .
View SolutionThe ratio of de-Broglie wavelength associated with a proton and a μ-particle accelerated through the same potential difference 'V' is
View SolutionThe de-Broglie wavelength associated with a particle of mass 10−6kg moving with a velocity of 10ms−1, is
View SolutionA particle of mass m and charge q travels from rest through a potential difference V. Its final energy is
View Solution

