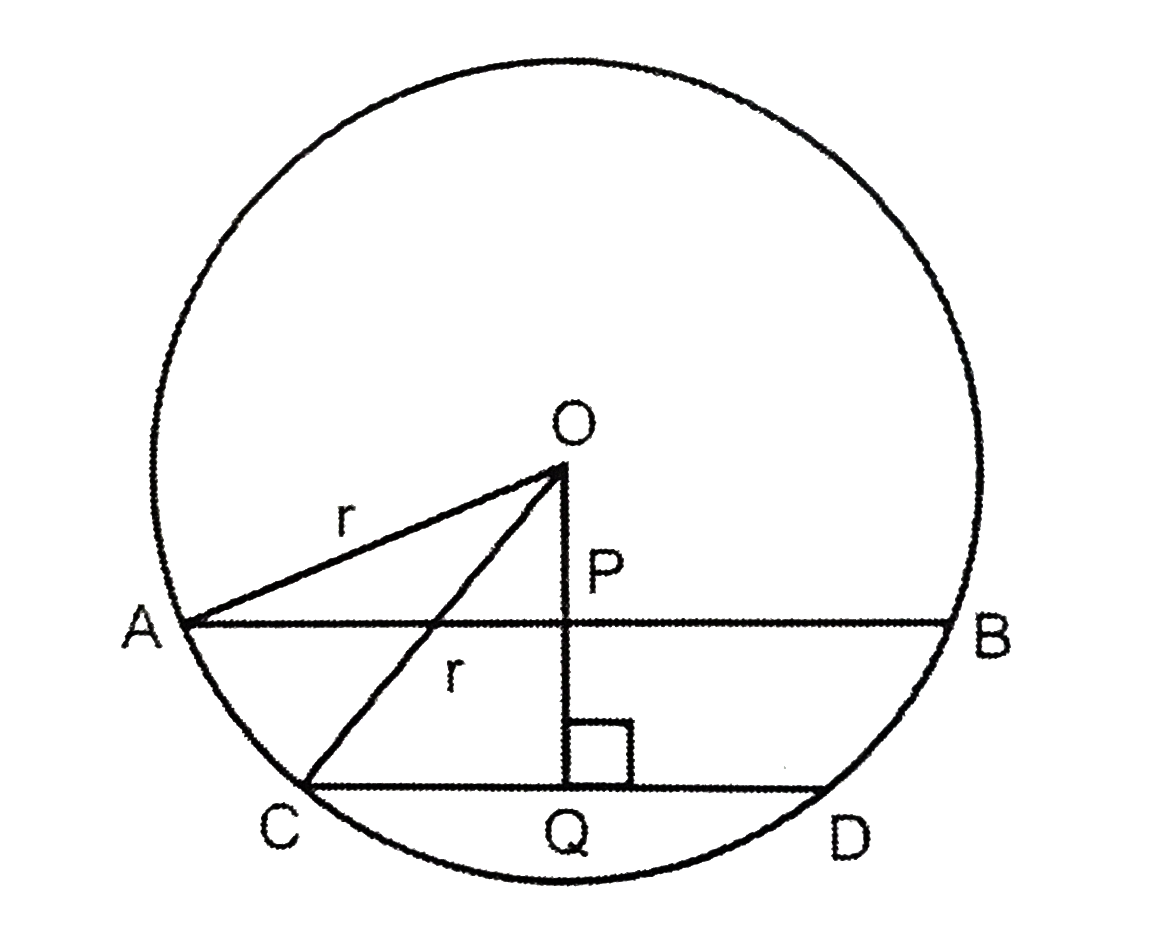
Two parallel chords of a circle, which are on the same side of centre,

2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.
A15 cm
B14 cm
C13 cm
D12 cm
Two parallel chords are drawn on the same side of the centre of a circle of radius R. It is found that they subtend and angle of $θ$ and $2 θ$ at the centre of the circle. The perpendicular distance between the chords is
A $2 R sin . \frac{3 θ}{2} sin . \frac{θ}{2}$
B $(1 - cos . \frac{θ}{2}) (1 + 2 cos . \frac{θ}{2}) R$
C $(1 + cos . \frac{θ}{2}) (1 - 2 cos . \frac{θ}{2}) R$
D $2 R sin . \frac{3 θ}{4} sin . \frac{θ}{4}$
The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
A4 cm
B5 cm
C6 cm
D8 cm

Two parallel chords of a circle, which are on the same side of centre,subtend angles of $72^{\circ} and 144^{\circ}$ respetively at the centre Prove that the perpendicular distance between the chords is half the radius of the circle.