Question

Figure shows the motion of a particle along a straight line. Find the average velocity of the particle during the intervals
(a)A to E , (b) B to E, (c ) C to E , (d) D to E , (e) C to D .

Explanation

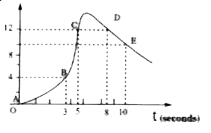
(a) As the particle moves from A to E, A is the initial point and E is the final point.
The slope of the line drawn from A to E
i.e., `(Deltax)/(Deltat)` gives the average velocity during that interval of time .
The displacement `Deltax` is
`X_E-X_A` = 10 cm -0 cm =+10 cm
The time interval `Deltat_(EA)=t_E-t_A` =10 s .
`therefore` During this interval average velocity
`barv=(Deltax)/(Deltat)=(+10cm)/(10s)=+1cms^(-1)`
(b)During the interval B to E , the displacement
`Deltax=x_E-x_B`=10 cm -4 cm =6 cm and `Deltat=t_E-t_B` =10s -3 s =7s
`therefore` Average velocity `barv=(Deltax)/(Deltat)=(6cm)/(7s)`
`=+0.857 cms^(-1) = 0.86 cms^(-1)`
(c) During the interval C to E , the displacement
`Deltax=x_E-x_C` = 10 cm -12 cm =2 cm and `Deltat=t_E-t_C` =10s - 5s =5s
`therefore barv=(Deltax)/(Deltat)=(-2cm)/(5s)=-0.4cms^(-1)`
(d)During the interval D to E , the displacement
`Deltax=x_E-x_D` = 10 cm -12 cm =-2cm
and the time interval
`Deltat=t_E-t_D` =10s -8s =2s
`therefore barv=(Deltax)/(Deltat)=(-2cm)/(2s)=-1cms^(-1)`
(e)During the interval C to D, the displacement
`Deltax=x_D-x_C` = 12cm -12cm =0
and the time interval `Deltat=t_D-t_C` =8s -5s =3s
`therefore` The average velocity `barv=(Deltax)/(Deltat)=(0m)/(3s)=0 ms^(-1)`
(The particle has reached the same position during these 3s. The average velocity is zero because the displacement is zero).