A car travels starting form rest with constant acceleration α and reaches a maximum velocity V. It travels with maximum velocity for some time and retards uniformly at the rate of β and comes to rest. If s is the total distance and t is the total time of journey then t=
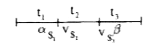
V=0+αt,t1=vα
S1=12αt21=v22α
O−V=βt3,t3=vβ
O2−V2=−2βS3
S3=v22β=12βt23
t2=S2V=S−(S1+S3)V=S−v22(1α+1β)V
t=t1+t2+t3
=vα+sv−v2α−v2β+vβ
t=sv+v2(α+βαβ)
s2=s−(s1+s2)=s−(v22α+v22α)
=s−v2α=s−(vt−s)
s2=2s−vt
[S2 = distance travelled with constant velocity]

Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -II
80 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
45 Videos
Similar Questions
A car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
View SolutionA car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
View Solution
Knowledge Check
A train starts from rest and moves with uniform acceleration α for some time and acquires a velocity v it then moves with constant velocity for some time and then decelerates at rate β and finally comes to rest at the next station. If L is distance between two stations then total time of travel is
ALV+V2(1α+1β)BLV−V2(1α+1β)CLV−V2(1α−1β)DLV+V2(1α−1β)A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβA car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
As=172ft2Bs=136ft2Cs=12ft2Ds=14ft2
A car, starating from rest, accelerates at the rate f through a distance S, then continoues at constant speed for time t and then decelerates as the rate f/2 to come to rest. If the total distance travelled is 15 S, then
View SolutionA car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
View SolutionA bus starting from rest, accelerates at the rate of f through a distance S, then continues at constant speed for time t and declerates at the rate f/2 to come to rest. If the total distance travelled is 15 S then S =
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA train accelerates from rest at a constant rate α for some time and then it retards to rest at the constant rate β. If the total distance covered by the train is s, then the velocity of the train is
View Solution
