A particle is projected form point O on the ground with velocity at angle . It strikes at a point C on a fixed smooth plane AB having inclination of with horizontal as shown is Fig. If the particle does not rebound , calculate .
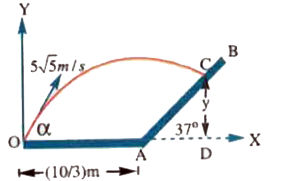
(a) coordinates of point C in reference t coordinate system as shown in the figure .
(b) maximum heing from the ground to which the particle reises.
(a) (b)
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - NUMERICAL EXERCISE (LEVEL -1)
33 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A particle is projected from point O on the ground with velocity u=5(√5)m/s at angle α=tan−1(0.5). It strikes at a point C on a fixed smooth plane AB having inclination of 37∘ with horizontal as shown in figure. If the particle does not rebound, calculate.
(a) coordinates of point C in reference to coordinate system as shown in the figure.
(b) maximum height from the ground to which the particles rises. (g=10m/s2)

View SolutionA particle is projected from point O on the ground with velocity u=5(√5)m/s at angle α=tan−1(0.5). It strikes at a point C on a fixed smooth plane AB having inclination of 37∘ with horizontal as shown in figure. If the particle does not rebound, calculate.
(a) coordinates of point C in reference to coordinate system as shown in the figure.
(b) maximum height from the ground to which the particles rises. (g=10m/s2)

View Solution
Knowledge Check
A particle is project d from point A with velocity u at an angle α with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
AutanαBucotαCucosαDucosecαA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
 A√3u2Bu2C2u√3Du
A√3u2Bu2C2u√3DuA particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
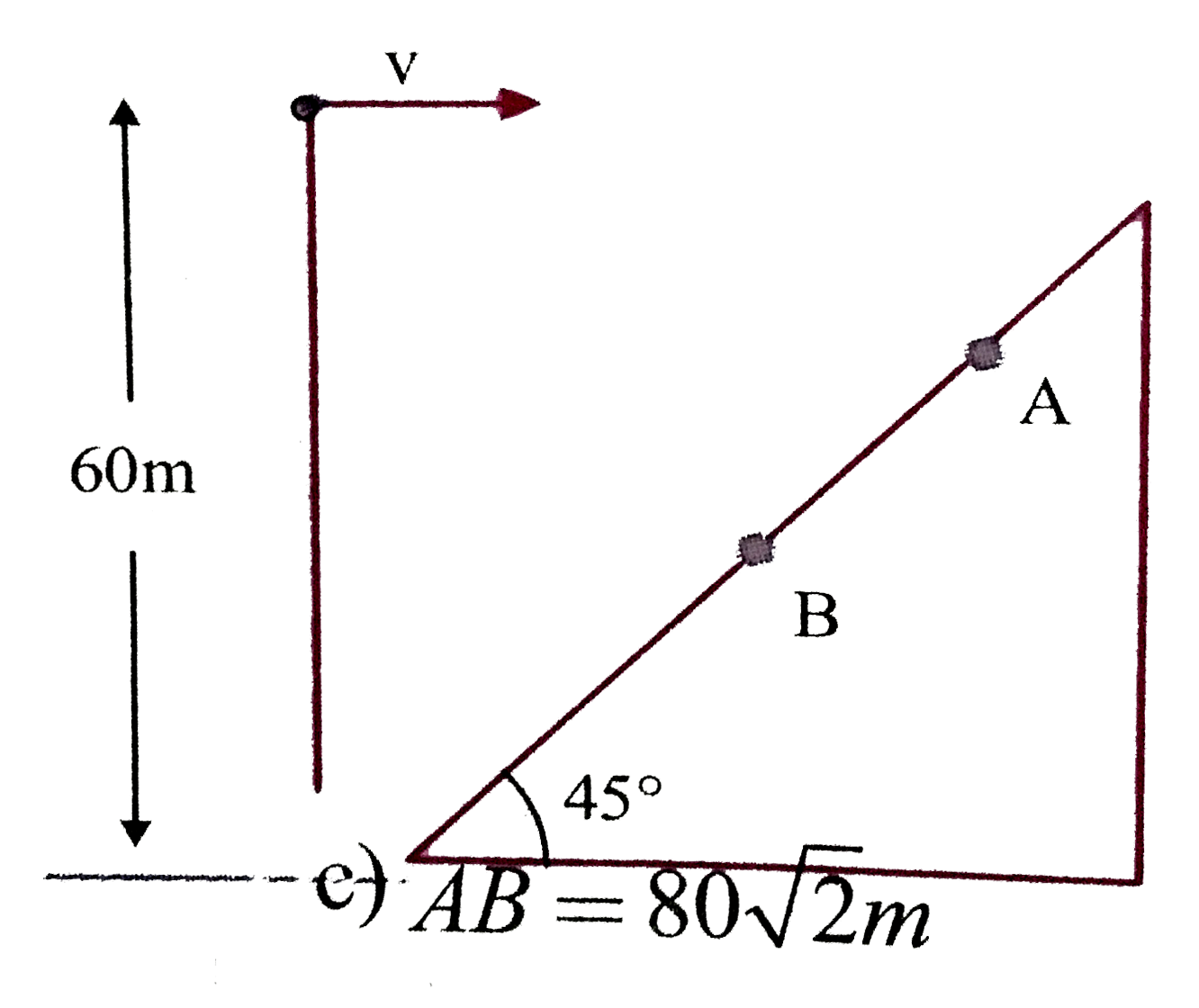 Av=20m/sBv=10m/sCAB=80√2mDAB=80m
Av=20m/sBv=10m/sCAB=80√2mDAB=80m
A particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA ball is projected from the point O with velocity 20 m/s at an angle of 60∘ with horizontal as shown in figure. At highest point of its trajectory it strikes a smooth plane of inclination 30∘ at point A. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is (g=10m/s2)

View SolutionA ball is projected from the point O with velocity 20 m/s at an angle of 60∘ with horizontal as shown in figure. At highest point of its trajectory it strikes a smooth plane of inclination 30∘ at point A. The collision is perfectly inelastic. The maximum height from the ground attained by the ball is (g=10m/s2)

View SolutionA particle is projected from point A perpendicular to inclined plane with a velocity 50m/s as shown in the figure. Particle strikes a vertical plane perpendicularly at point B. Time taken by particle in going from point A to point B is
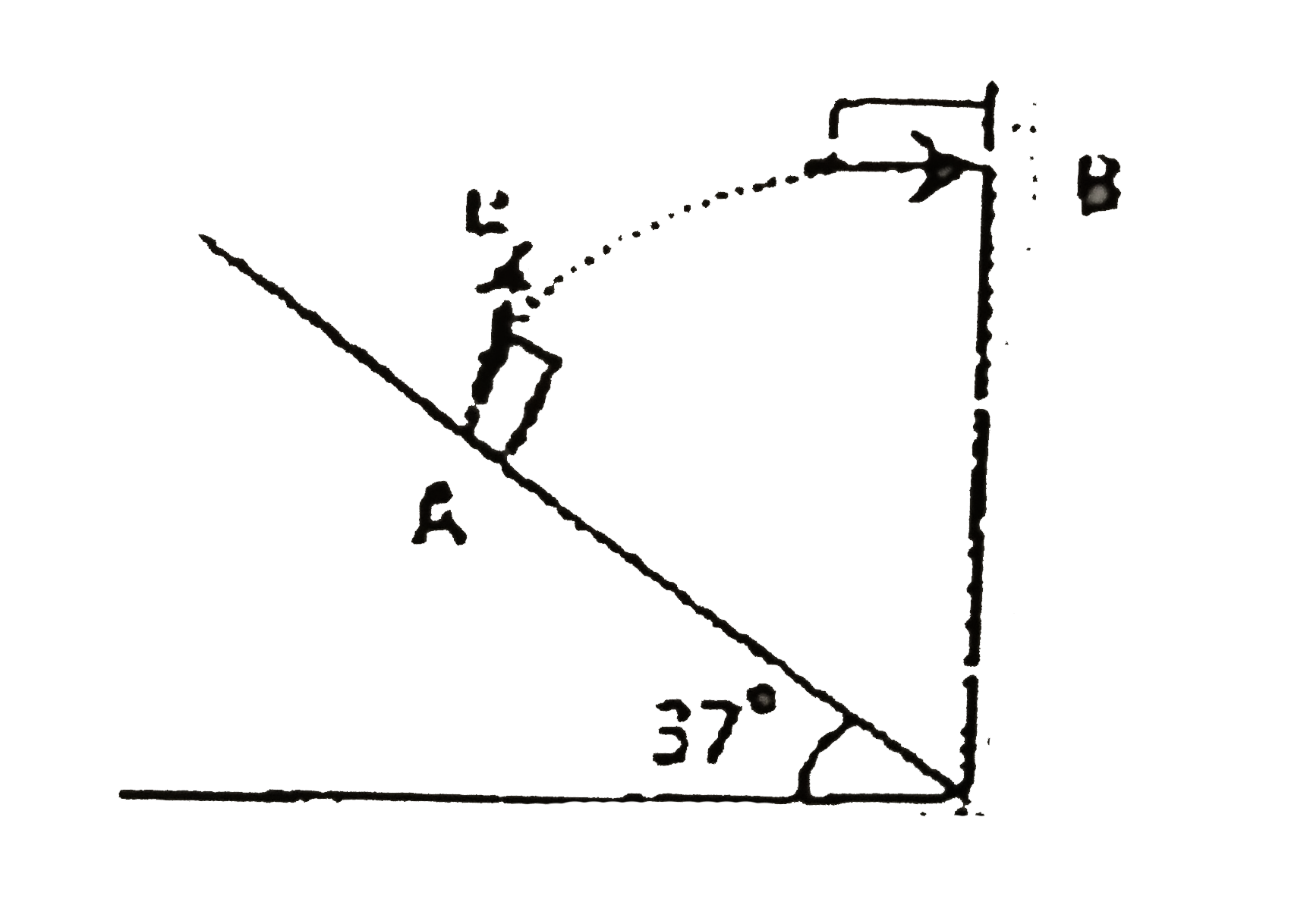
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
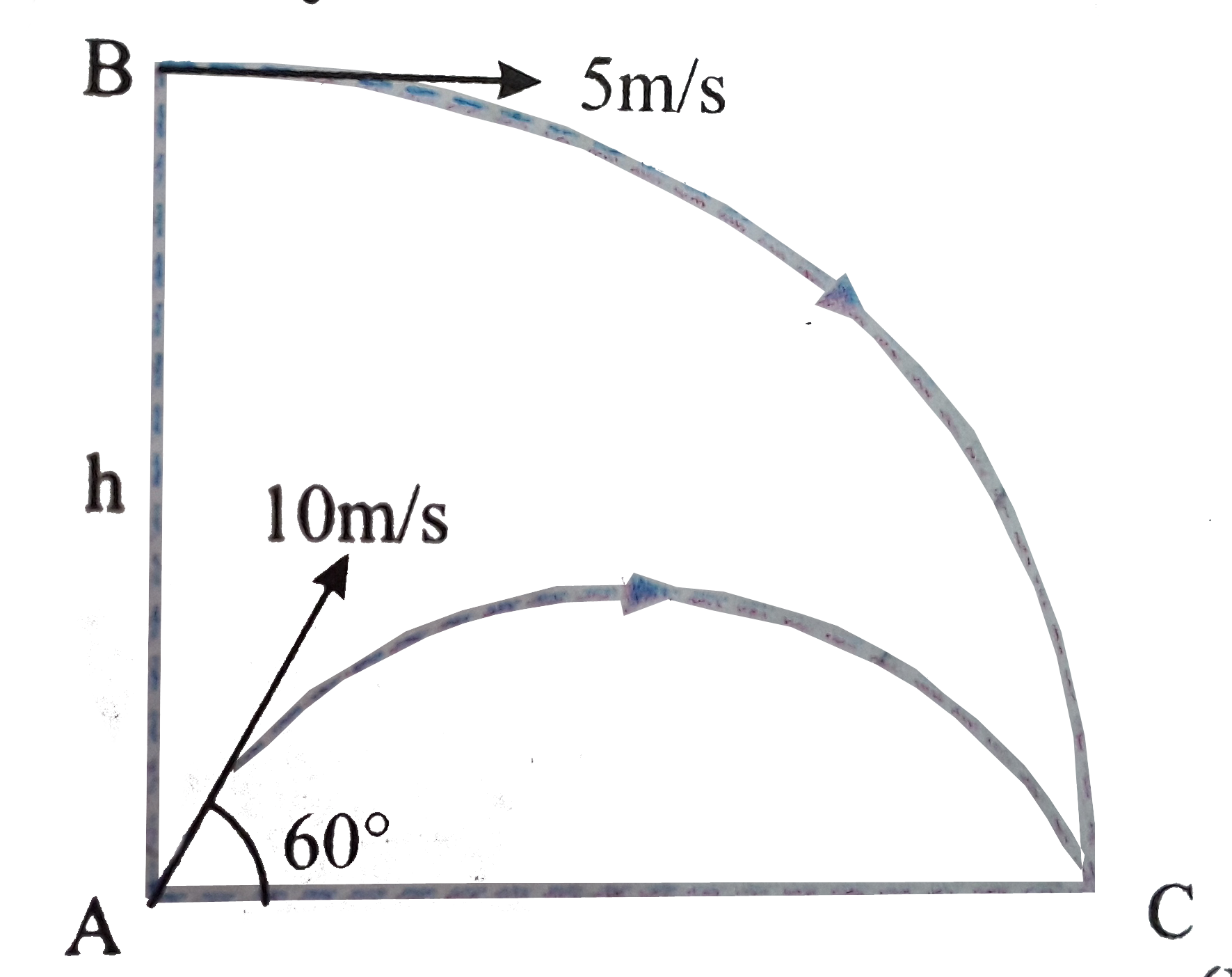
View Solution
