Question

(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic field in accelerating the charge. Hence , derive the expression for the kinetic energy aquired by the particles.
(b) An $\alpha$- particle and proton are released from the center of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency? Give resons to justify your answer.
(ii) when they are accelerated in turn, which of the two will have higher velocity at the exit slit of the dees?

Explanation

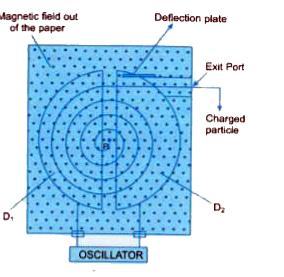
(a) Labelled diagram of cyclotron is shown in Fig.
(b) Principle : (i) A Positively changed ion can be accelerated to a high energy with help of smaller values of oscillating electric field by making it to cross the same electric filed time and again .
(ii) A charged ion moving perpendicular to a magnetic field describes a circular path.
Working : The ion produced at P is accelerated towards the dee `(D_1` say) which is at a negative potential at that instant. Inside dee `D_1` the ion describes a semi-circular path with a constant speed (say `v`) such that radius of circular path is given by
`r = (mv)/(Bq)` and time taken by the ion to describe a semi - circular path
`t = (pi r)/(v) = (pi m)/(Bq) ` = a constant.
According to cyclotron condition if during this time t the direction of oscillating electric field just gets reversed, the ion will be further accelerated towards dee `D_2` and describe a bigger semi-circular path inside `D_2` and so on. If v be the frequency of oscillating electric field, then
`t = (pi m)/(B q) = 1/(2v) " or " v = (Bq)/(2 pi m)`
This frequency of oscillating electric field is commonly referred as the cyclotron frequency. From the expression it is clear that the cyclotron frequency depends on magnetic field B as well as the charge and mass of ion beam to be accelerated. However, the cyclotron frequency is independent of hte speed of the charged particle or radius of semi-circular path described by them.
When the radius of circular path of ion becomes almost equal to the radius of dees, it is taken out through an exit port. If R = maximum radius of ion path then maximum energy acquired by the ion
`K_("max") = 1/2 mv_("max")^(2) = 1/2 m ((BqR)/(m))^(2) = (B^2 q^2 R^2)/(2m)`.
(b) (i) As cyclotron frequency depends on both charge and mass of ion to be accelerated, it is obvious that an a-particle and a proton cannot be accelerated at the same cyclotron frequency.
(ii) As `r = (mv)/(qB)`
Hence, at the exit slit of hte dees of a cyclotron `v = (qBR)/(m)`
As `(q/m)_("proton") > (q/m)_(alpha - "particle")` , the proton will have higher velocity thant alpha particle.