(a) Briefly describe the Young's double-slit experiment of interference of light. Derive the expression for fringe width in the pattern.
(b) Monochromatic light of wavelength 588 nm is incident from air to water interface. Find the wavelength and speed of the refracted light. The refractive index of water is $\frac{4}{3}$ .

Text Solution

Verified by Experts

The correct Answer is:a

(a) A simple schematic diagram of Young.s double-slit experiment to produce interference pattern due to a monochromatic source of light is shown here. Let $S_{1}$ and $S_{2}$ be two narrow slits, a small distance .d. apart, illuminated by a monochromatic light source S of wavelength $λ$ , kept equidistant from the slits $S_{1}$ and $S_{2}$ and MN be a screen situated at a distance .D. from double-slit and it is parallel to double-slit. Then, we obtain alternate bright and dark fringes on the screen and the central point O of the screen is bright. Consider a point P on the screen MN, at a distance .x. from the symmetrical central point O of screen. Path difference between

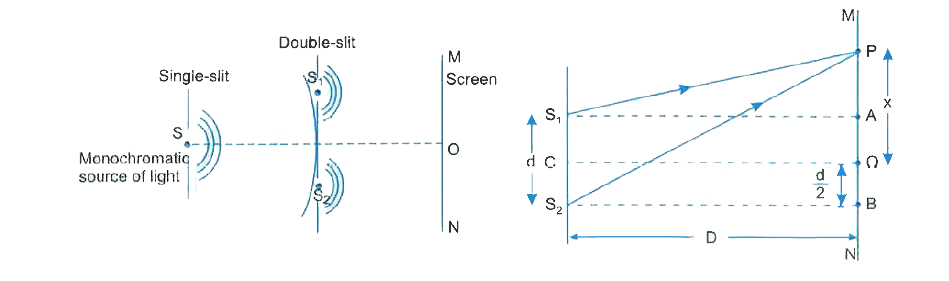
light waves reaching point P from two slit sources is $S_{2} P - S_{1} P$ , where
${(S_{2} P)}_{2}^{2} = D^{2} + {(x + \frac{d}{2})}^{2}$ and ${(S_{1} P)}_{1}^{2} = D^{2} + {(x - \frac{d}{2})}^{2}$
$∴ {(S_{2} P)}_{2}^{2} - {(S_{1} P)}_{1}^{2} = [D^{2} + {(x + \frac{d}{2})}^{2}] - [D^{2} + {(x - \frac{d}{2})}^{2}] = 2 x d$
$\Rightarrow (S_{2} P - S_{1} P) (S_{2} p + S_{1} P) = 2 x d$
or $(S_{2} P - S_{1} P) = \frac{2 x d}{(S_{2} P + S_{1} P)}$
If x and dare very very small as compared to D, then $(S_{2} P + S_{1} P)$ may be considered as 2D. Hence,
$[S_{2} P - S_{1} P] = \frac{2 x d}{2 D} = \frac{x d}{D}$
For constructive interference, path difference must be an integer multiple of $λ$ i.e., $\frac{x d}{D} = n λ$ where n = 0, 1, 2, 3, ... etc.
$∴ x = \frac{n D λ}{d}$ i.e., positions of various maxima (bright bands) will be given by :
$x_{0} = 0, x_{1} = \frac{D λ}{d}, x_{2} = \frac{2 D λ}{d}, x_{3} = \frac{3 D λ}{d}$ ........
For destructive interference, path difference must be an odd multiple of $\frac{λ}{2}$ i.e., $\frac{x d}{D} = (2 n - 1) \frac{λ}{2}$ , where n ::= 1, 2, 3, ... etc.
$\Rightarrow x = \frac{(2 n - 1) D λ}{2 d}$ i.e., positions of various minima (dark bands) will be given by :
$x_{1} . = \frac{D λ}{2 d}, x_{2} . = \frac{3 D λ}{2 d}, x_{3} . = \frac{5 D λ}{2 d}$ ......
Fringe width of the fringe pattern is defined as the distance between two successive maxima or successive minima. Therefore, considering two successive maxima, we have
Fringe width $β = x_{n + 1} - x_{n} = \frac{(n + 1) D λ}{d} - \frac{n D λ}{d} = \frac{D λ}{d}$
(b) Here wavelength $λ$ = 588 nm and refractive index of water w.r.t. air $n = \frac{4}{3}$
We know that speed of light in air = $c = 3 \times 10^{8} m s^{- 1}$
$∴$ Speed of light in water v = $\frac{c}{n} = \frac{3 \times 10^{8}}{(4 / 3)} = 2.25 \times 10^{8} m s^{- 1}$
and wavelength of given light in water, $λ_{w} = \frac{λ}{n} = \frac{588 n m}{(4 / 3)} = 441 n m$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

A beam o monochromatic light of wavelength $λ$ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
A $\frac{9}{16} \times λ$
B $3 λ / 4$
C $λ \times \frac{4}{3}$
D $λ$
Interference fringes in Young's double slit experiment with monochromatic light are
Aalways equispaced
Balways unequally spaced
Cboth equally and unequally spaced
Dformed by a portion of the wave front.

U-LIKE SERIES-EXAMINATION PAPER 2020 (SOLVED)-SECTION D

Home
Ask Doubt
Profile