Find (lim)x→5f(x), where f(x)=|x|−5
To find the limit limx→5f(x) where f(x)=|x|−5, we can follow these steps:
Step 1: Understand the function
The function f(x)=|x|−5 is defined for all x. Since we are interested in the limit as x approaches 5, we will evaluate the function around this point.
Step 2: Calculate the left-hand limit
To find the left-hand limit as x approaches 5, we consider values of x that are slightly less than 5. Thus, we can express this as:
limx→5−f(x)=limx→5−(|x|−5)
Since x is approaching 5 from the left, x is positive, so |x|=x. Therefore:
limx→5−f(x)=limx→5−(x−5)
Now, substituting x=5:
limx→5−(x−5)=5−5=0
Step 3: Calculate the right-hand limit
Next, we calculate the right-hand limit as x approaches 5, which considers values of x that are slightly greater than 5:
limx→5+f(x)=limx→5+(|x|−5)
Again, since x is approaching 5 from the right, x is still positive, so |x|=x. Therefore:
limx→5+f(x)=limx→5+(x−5)
Substituting x=5:
limx→5+(x−5)=5−5=0
Step 4: Conclude the limit
Since both the left-hand limit and the right-hand limit are equal, we can conclude that:
limx→5f(x)=0
Thus, the final answer is:
limx→5f(x)=0
---
The function f(x)=|x|−5 is defined for all x. Since we are interested in the limit as x approaches 5, we will evaluate the function around this point.
To find the left-hand limit as x approaches 5, we consider values of x that are slightly less than 5. Thus, we can express this as:
limx→5−f(x)=limx→5−(|x|−5)
Since x is approaching 5 from the left, x is positive, so |x|=x. Therefore:
limx→5−f(x)=limx→5−(x−5)
Now, substituting x=5:
limx→5−(x−5)=5−5=0
Next, we calculate the right-hand limit as x approaches 5, which considers values of x that are slightly greater than 5:
limx→5+f(x)=limx→5+(|x|−5)
Again, since x is approaching 5 from the right, x is still positive, so |x|=x. Therefore:
limx→5+f(x)=limx→5+(x−5)
Substituting x=5:
limx→5+(x−5)=5−5=0
Since both the left-hand limit and the right-hand limit are equal, we can conclude that:
limx→5f(x)=0
limx→5f(x)=0
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - SOLVED EXAMPLES
25 Videos
- LIMITS AND DERIVATIVESBOOK - NCERT ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - MISCELLANEOUS EXERCISE
30 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.1
4 Videos
- LINEAR INEQUALITIESBOOK - NCERT ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - EXERCISE 6.2
10 Videos
Similar Questions
Find (lim)x→1f(x) ,where f(x)={x2−1x≤1−x2−1x>1
View SolutionFind (lim)x→3 f(x) where f(x)={4, if x>3x+1, if x<3
View SolutionFind limx→1f(x), where f(x)={x+1x≠10x=1}
View SolutionFind limx→0f(x), where f(x)=⎧⎪⎨⎪⎩x−1x<00x=0x=1x>0
View SolutionFind limx→0f(x) where
f(x)={x|x|x≠00x=0
View SolutionFind limX→0f(x) where f(x)={xx≠05x=0}
View SolutionIf f(x) is differentiable at x=a , find (lim)x→ax2f(a)−a2 f(x)x−a .
View SolutionCalculate limx→0f(x), where f(x)=1x2 for x>0
View SolutionLet f(x)=x2−9x+20x−[x] (where [x] is the greatest integer not greater than x. Then (A)(lim)x→5f(x)=1 (B) (lim)x→5f(x)=0 (C) (lim)x→5f(x) does not exist. (D)none of these
View SolutionEvaluate limx→0f(x), where
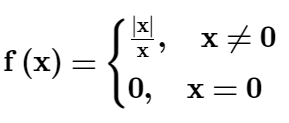
View Solution
