In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
To solve the problem, we need to find the probability that a randomly selected student from the class is studying either Mathematics or Biology. We can use the formula for the probability of the union of two events.
1. Define the Variables:
Let x be the total number of students in the class.
2. Calculate the Number of Students Studying Mathematics:
Given that 40% of the students study Mathematics, the number of students studying Mathematics is:
Number of students studying Mathematics=0.40x=4x10
3. Calculate the Number of Students Studying Biology:
Given that 30% of the students study Biology, the number of students studying Biology is:
Number of students studying Biology=0.30x=3x10
4. Calculate the Number of Students Studying Both Subjects:
Given that 10% of the students study both Mathematics and Biology, the number of students studying both is:
Number of students studying both=0.10x=x10
5. Calculate the Probabilities:
- Probability of a student studying Mathematics (P(M)):
P(M)=Number of students studying Mathematicsx=4x/10x=410=0.4
- Probability of a student studying Biology (P(B)):
P(B)=Number of students studying Biologyx=3x/10x=310=0.3
- Probability of a student studying both Mathematics and Biology (P(M∩B)):
P(M∩B)=Number of students studying bothx=x/10x=110=0.1
6. Use the Formula for the Probability of the Union of Two Events:
The probability that a student studies either Mathematics or Biology (P(M∪B)) is given by:
P(M∪B)=P(M)+P(B)−P(M∩B)
Plugging in the values we calculated:
P(M∪B)=0.4+0.3−0.1=0.6
7. Final Answer:
Therefore, the probability that a randomly selected student studies either Mathematics or Biology is:
P(M∪B)=0.6
Let x be the total number of students in the class.
Given that 40% of the students study Mathematics, the number of students studying Mathematics is:
Number of students studying Mathematics=0.40x=4x10
Given that 30% of the students study Biology, the number of students studying Biology is:
Number of students studying Biology=0.30x=3x10
Given that 10% of the students study both Mathematics and Biology, the number of students studying both is:
Number of students studying both=0.10x=x10
- Probability of a student studying Mathematics (P(M)):
P(M)=Number of students studying Mathematicsx=4x/10x=410=0.4
- Probability of a student studying Biology (P(B)):
P(B)=Number of students studying Biologyx=3x/10x=310=0.3
- Probability of a student studying both Mathematics and Biology (P(M∩B)):
P(M∩B)=Number of students studying bothx=x/10x=110=0.1
The probability that a student studies either Mathematics or Biology (P(M∪B)) is given by:
P(M∪B)=P(M)+P(B)−P(M∩B)
Plugging in the values we calculated:
P(M∪B)=0.4+0.3−0.1=0.6
Therefore, the probability that a randomly selected student studies either Mathematics or Biology is:
P(M∪B)=0.6
Topper's Solved these Questions
Similar Questions
In a class of 60 students, 30 opted for Mathematics, 32 opted for Biology and 24 opted for both Mathematics and Biology. If one of these students is selected at random, find the probability that :
(i) The students opted for Mathematics or Biology.
(i) The students has opted neither Mathematics nor Biology.
(iii) The students has opted Mathematics but not Biology.
View SolutionA class has 20 girls and 16 boys. One student is selected at random. Find the probability that the student is a girl.
View Solution
Knowledge Check
A class has 12 boys and 4 girls. If three students are selected at random from the class,
what is the probability that all will be boys?A155B14C13D1128
There are 60% students in Maths and 30% in Biology. If 10% students are in both subjects. Find the probability that a randomly selected student has Maths or Biology.
View SolutionIn a school 25% students are failed in Mathematics, 15% in Physics and 5% students fail in both Mathematics and Physics. A student is selected at random.
(i) If he is fail in Physics, find the probability that he is fail in Mathematics.
(ii) If he is fail in Mathematics, find the probability that he in fail in Physics.
(iii) Find the probability that he is fail either in Mathematics or in Physics.
View SolutionIn a class of 50 students, 20 are boys and rest are girls. A student is selected at random. Find the probability of selecting a boy.
View SolutionIn a class, 5% of the boys and 10% of the girls have an IQ of more than 150. In this class 60% of the students are boys. If a student is selected at random and found to have an IQ of more than 150, find the probability that the student is a boy.
View SolutionIn a medical examination of students of a class, the following blood groups are recorded.
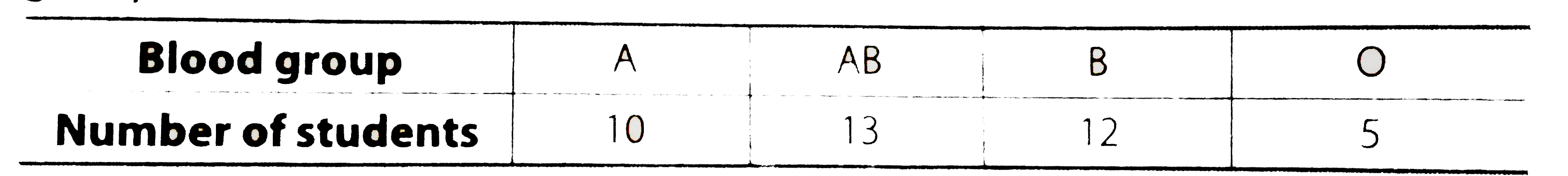
A student is selected at random from the class. The probability that he/she has blood group B, is
View SolutionIn a college, 30% students fail in physics, 25% fail in Mathematics and 10% in both. One student is choosen at random. The probability that she fails in physics, if she has failed in Mathematics is
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passed in only one subject.
View Solution
