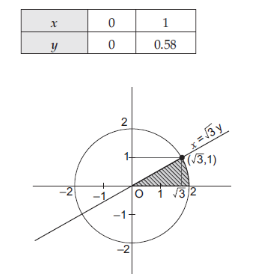
Prove that the area in the first quadrant enclosed by the axis, the line $x = \sqrt{3} y$ and the circle $x^{2} + y^{2} = 4 i s π / 3 .$

Video Solution

Text Solution

Verified by Experts

Obviously $x^{2} + y^{2} = 4$ is a
circle having centre at $(0, 0)$ and radius $2$ units.
For graph of line x $= \sqrt{3} y$
For intersecting point of given circle and line
putting $x = \sqrt{3} y in x^{2} + y^{2} = 4$
we get
${(\sqrt{3} y)}^{2} + y^{2} = 4$
$3 y^{2} + y^{2} = 4$
$4 y^{2} = 4$
$y = \pm 1$ , $y = \pm 1$
Intersecting points are $(\sqrt{3}, 1), (- \sqrt{3}, - 1)$
Shaded region is required region
Now required area $= \int_{0}^{\sqrt{3}} \frac{x}{\sqrt{3}} d x + \int_{\sqrt{3}}^{2} \sqrt{4 - x^{2}}$
$= \frac{1}{\sqrt{3}} {[\frac{x^{2}}{2}]}_{0}^{\sqrt{3}} + {[\frac{x \sqrt{4 - x^{2}}}{2} + \frac{4}{2} {sin}^{- 1} (\frac{x}{2})]}_{\sqrt{3}}^{2}$
$= \frac{1}{2 \sqrt{3}} (3 - 0) + [2 {sin}^{- 1} (1) - (\frac{\sqrt{3}}{2} + 2 {sin}^{- 1} (\frac{\sqrt{3}}{2})]$
$= \frac{\sqrt{3}}{2} + [2 (\frac{π}{2}) - \frac{\sqrt{3}}{2} - \frac{2 π}{3}]$
$= \frac{\sqrt{3}}{2} + π - \frac{\sqrt{3}}{2} - \frac{2 π}{3}$
$= π - \frac{2 π}{3} = \frac{π}{3}$ sq.unit

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile