(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North–South direction and East–West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are about 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines. There are many cross– streets in your model. A particular cross–street is made by two streets, one running in the North – South direction and another in the East – West direction. Each cross street is referred to in the following maimer : If the 2nd street running in the North – South direction and 5th in the East – West direction meet at some crossing, then we will call this cross–street (2. 5). Using this convention, find:(i) how many cross – streets can be referred to as (4, 3).(ii) how many cross – streets can be referred to as (3, 4).
a) are cross points
b) only one cross point.
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - NCERT ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Solved Examples
4 Videos
- COORDINATE GEOMETRYBOOK - NCERT ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.2
2 Videos
- CONSTRUCTIONSBOOK - NCERT ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.2
5 Videos
- HERONS FORMULABOOK - NCERT ENGLISHCHAPTER - HERONS FORMULAEXERCISE - Solved Examples
6 Videos
Similar Questions
Knowledge Check
Arrange the cities from East to West
ACairoBTehranCTripoliDBaghdadIf North direction is called East and South direction is called West, then what will be called North - East direction ?
ANorth EastBEast - SouthCWest SouthDNorth - WestThe streets of a city are arranged like the lines of a chess board . There are m streets running North to South and 'n' streets running East to West . The number of ways in which a man can travel from NW to SE corner going the shortest possible distance is
A√m2+n2B√(m−1)2.(n−1)2C(m+n)!m!.n!D(m+n−2)!(m−1)!.(n−1)!
A rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View SolutionA rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View SolutionThe streets of city are arranged like the lines of a chess board. There are 5 streets runnings North to South & '3' streets running East to West. The numberof ways is which a man can travel from NW to SE corner going the shortest possible ditance is :
View SolutionA rectangular grass plot 80m×60m has two roads, each 10 m wide, running in the middle of it, one parallel to length and the other parallel to breadth.Find the area of the roads.
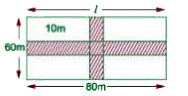
View SolutionThe streets of city are arranged like the lines of a chess board. There are 5 streets runnings North to South & '3' streets running East to West. The numberof ways is which a man can travel from NW to SE corner going the shortest possible ditance is :
View Solution
