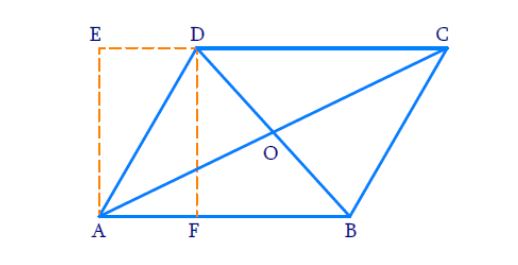
Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.

Video Solution

Text Solution

Verified by Experts

Let, ABCD is a parallelograma
$A B = C D$ , $A D = B C$ [Since opposite sides of a parallelogram are equal]
AC and BD are the diagonals of the parallelogram ABCD
Draw $A E ⊥ C D$ , $D F ⊥ A B$
We have to prove that, $A C^{2} + B D^{2} = A B^{2} + B C^{2} + C D^{2} + A D^{2}$
$E A = D F$ (Perpendiculars drawn between same parallel lines)
According to Pythagoras theorem,
In $Δ A E C$
$A C^{2} = A E^{2} + E C^{2}$
$A C^{2} = A E^{2} + {(E D + D C)}^{2}$ [Since EC = ED + DC]
$A C^{2} = A E^{2} + D E^{2} + D C^{2} + 2 D E . D C$ [Since ${(a + b)}^{2} = a^{2} + b^{2} + 2 a b$ ]
$A C^{2} = A D^{2} + D C^{2} + 2 D E . D C$ .....(i) [Since, $A D^{2} = A E^{2} + D E^{2}$ in ΔAED]
In ΔDFB
$B D^{2} = D F^{2} + B F^{2}$
$B D^{2} = D F^{2} + {(A B - A F)}^{2}$ [Since $B F = A B = A F$ ]
$B D^{2} = D F^{2} + A B^{2} + A F^{2} - 2 A B . A F$ [Since ${(a - b)}^{2} = a^{2} + b^{2} - 2 a b$ ]
$B D^{2} = A D^{2} + A B^{2} - 2 A B . A F$ .....(ii) [Since, $A D^{2} = D F^{2} + A F^{2}$ in ΔAFD]
Adding (i) and (ii)
$A C^{2} + B D^{2} = A D^{2} + D C^{2} + 2 D E . D C + A D^{2} + A B^{2} - 2 A B . A F$
$A C^{2} + B D^{2} = B C^{2} + D C^{2} + 2 A B . A F + A D^{2} + A B^{2} - 2 A B . A F$ [Since $A D = B C$ and $D E = A F$ , $C D = A B$ ]
Thus, $A C^{2} + B D^{2} = A B^{2} + B C^{2} + C D^{2} + A D^{2}$

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

NCERT ENGLISH-TRIANGLES-Exercise 6.1

Home
Ask Doubt
Profile