100 surnames were randomly picked up from a local telephone directly and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows: Number of letters: 1-4 4-7 7-10 10-13 13-16 16-19 Number surnames 6 30 40 16 4 4 Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, find the modal size of the surnames.
1) median class = 7 - 10
Class size, h = 3
Lower limit of median class, l = 7
Frequency of median class, f = 40
Cumulative frequency of class preceding median class,cf=36
Median = l+[n2−cff]×h
= 7+[50−3640]×3
= 7+(1440)×3
= 7+2120
= 7+1.05
=8.05
2)Now, we will find the mean.
Class mark, xi= (Upper class limit + Lower class limit)/2
Taking assumed mean, a = 11.5
Σfi = 100 andΣfiui = -106
Class size, h=3
Mean, (x) = a+(ΣfiuiΣfi)×h
=11.5+(−106100)×3
=11.5−318100
=11.5−3.18
8.32
3)it can be observed that the maximum class frequency is 40, belonging to class interval 7−10.
Class size, h=3
Modal class =7−10
Lower limit of modal class, l=7
Frequency of modal class, f1=40
Frequency of class preceding modal class, f0=30
Frequency of class succeeding the modal class, f2=16
Mode =l+[f1−f02f1−f0−f2]×h
=7+[40−302×40−30−16]×3
=7+(1034)×3
=7+1517
=7+0.88
=7.88
=8.05
Similar Questions
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letter in English alphabet in the surnames was found as follows:
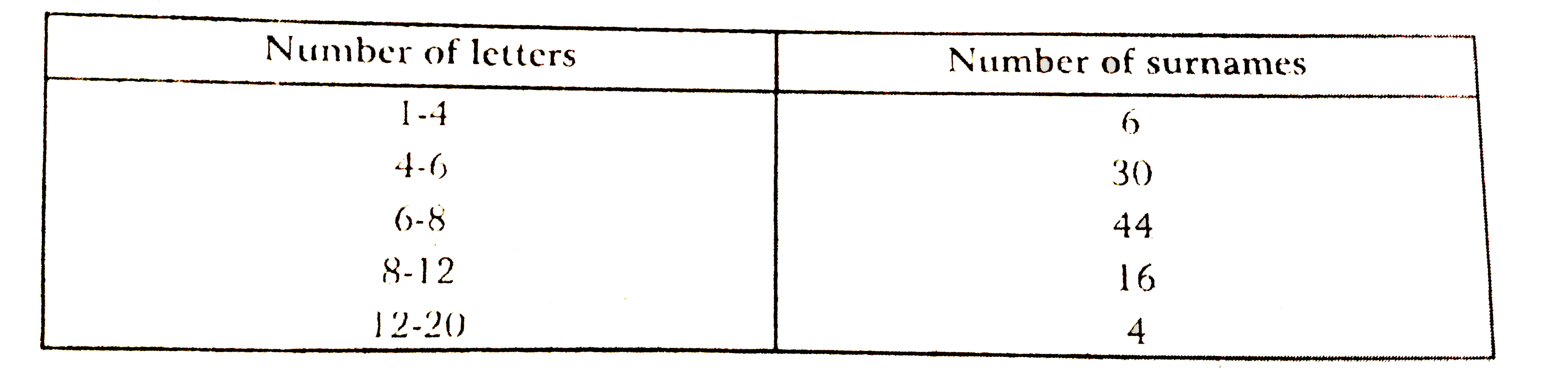
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
View SolutionFind the number of terms in the sequence 4,7,10,13…….,82.
View SolutionFind the total number of permutations of the letters of the word INSTITUTE.
View SolutionTwo letters are drawn from the english alphabets.
Find the probability that both letters are vowels.
View SolutionFind the number of permutations of the letters of the word ALLAHABAD.
View SolutionHow many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
View SolutionFind the number of arrangements of the letters of the EXAM
View SolutionWrite the set of the letter of the word 'ALLAHABAD'. Also find the number of subsets of this set.
View SolutionWrite the set of the letter of the word 'ALLAGABAD'. Also find the number of subsets of this set.
View SolutionFind the number of permutations of the letters of the word PRE-UNIVERSITY.
View Solution
