A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30∘to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60∘ to the ground. What should be the length of the slide in each case?
To solve the problem of finding the lengths of the slides for children in the park, we will use the properties of right triangles and trigonometric ratios.
1. Identify the Problem:
We have two slides:
- Slide for children below 5 years: Height = 1.5 m, Angle of inclination = 30°.
- Slide for elder children: Height = 3 m, Angle of inclination = 60°.
2. Draw the Diagram:
For both slides, we can visualize a right triangle where:
- The height of the slide is the opposite side (perpendicular).
- The length of the slide is the hypotenuse.
- The angle of inclination is given.
3. Calculate the Length of the Slide for Younger Children:
- For the slide with height 1.5 m and angle 30°:
- Using the sine function:
sin(θ)=OppositeHypotenuse
- Here, θ=30°, Opposite = 1.5 m, and Hypotenuse = length of the slide (let's denote it as L1):
sin(30°)=1.5L1
- We know that sin(30°)=12:
12=1.5L1
- Cross-multiplying gives:
L1=1.5×2=3 m
4. Calculate the Length of the Slide for Elder Children:
- For the slide with height 3 m and angle 60°:
- Again using the sine function:
sin(60°)=OppositeHypotenuse
- Here, θ=60°, Opposite = 3 m, and Hypotenuse = length of the slide (let's denote it as L2):
sin(60°)=3L2
- We know that sin(60°)=√32:
√32=3L2
- Cross-multiplying gives:
L2=3×2√3=6√3=2√3 m
5. Final Results:
- Length of the slide for younger children: 3 m
- Length of the slide for elder children: 2√3 m
We have two slides:
- Slide for children below 5 years: Height = 1.5 m, Angle of inclination = 30°.
- Slide for elder children: Height = 3 m, Angle of inclination = 60°.
For both slides, we can visualize a right triangle where:
- The height of the slide is the opposite side (perpendicular).
- The length of the slide is the hypotenuse.
- The angle of inclination is given.
- For the slide with height 1.5 m and angle 30°:
- Using the sine function:
sin(θ)=OppositeHypotenuse
- Here, θ=30°, Opposite = 1.5 m, and Hypotenuse = length of the slide (let's denote it as L1):
sin(30°)=1.5L1
- We know that sin(30°)=12:
12=1.5L1
- Cross-multiplying gives:
L1=1.5×2=3 m
- For the slide with height 3 m and angle 60°:
- Again using the sine function:
sin(60°)=OppositeHypotenuse
- Here, θ=60°, Opposite = 3 m, and Hypotenuse = length of the slide (let's denote it as L2):
sin(60°)=3L2
- We know that sin(60°)=√32:
√32=3L2
- Cross-multiplying gives:
L2=3×2√3=6√3=2√3 m
- Length of the slide for younger children: 3 m
- Length of the slide for elder children: 2√3 m
Similar Questions
A carpenter makes stools for electricians with a square top of side 0.5m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60∘ to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
View SolutionThe speed of a homogenous solid sphere after rolling down an inclined plane of vertical height h, from rest without sliding is
View SolutionAn electrician has to repair an electric fault on a pole of height 5 m. She needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60° to the horizontal, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder? (You may take √3 = 1.73)
View SolutionFor a block of mass m to slide without friction up the rise of height h shown, it must have a minimum initial speed of:
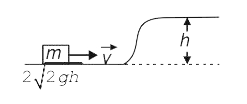
View SolutionThe speed of a uniform solid cylinder after rolling down an inclined plane of vertical height H, from rest without sliding is :-
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionThe present age of a father is equal to the sum of the ages of his 5 children. 12 years hence, the sum of the ages of his children will be twice the ages of their father. Find the present age of the father.
View SolutionIf the inclination of an inclined plane is 30∘, a block of mass m kept at rest on the surface of the plane, will just slide down. If the inclination is raised to 45∘ what will be the acceleration of the body ?
View SolutionA block is placed at the top of an inclined plane 5 m long. The plane makes an angle of 60∘ with the horizontal. If the coefficient of friction between the wood and the plane is 0.3, find the time taken by the block of slide down the bottom of the plane.
View SolutionA block slides down a frictionless, inclined plane that makes a 30∘ angle with the horizontal. Find the acceleration of this block.
View Solution
