Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
To prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle, we can follow these steps:
Step 1: Understand the Setup
Let ABCD be a quadrilateral that circumscribes a circle with center O. The sides AB, BC, CD, and DA are tangent to the circle at points P, Q, R, and S respectively.
Step 2: Draw Radii and Tangents
Draw the radii from the center O to the points of tangency:
- OP is perpendicular to AB
- OQ is perpendicular to BC
- OR is perpendicular to CD
- OS is perpendicular to DA
Step 3: Identify Angles
We need to show that the angles subtended by the opposite sides at the center O are supplementary. Specifically, we will show that:
∠BOC+∠AOD=180∘
Step 4: Use Properties of Tangents
From the properties of tangents, we know that:
- AP=AS (tangents from point A)
- BP=BQ (tangents from point B)
- CQ=CR (tangents from point C)
- DR=DS (tangents from point D)
Step 5: Relate Angles
Using the tangent properties, we can express the angles at the center:
- ∠AOB=∠APB+∠BQA
- ∠COD=∠CRD+∠DSA
Step 6: Sum of Angles in Quadrilateral
The sum of angles around point O in quadrilateral ABCD is:
∠AOB+∠BOC+∠COD+∠DOA=360∘
Since opposite angles are equal, we can simplify:
∠AOB+∠COD=180∘
This implies:
∠BOC+∠AOD=180∘
Conclusion
Thus, we have shown that the opposite sides of the quadrilateral ABCD subtend supplementary angles at the center O.
---
Let ABCD be a quadrilateral that circumscribes a circle with center O. The sides AB, BC, CD, and DA are tangent to the circle at points P, Q, R, and S respectively.
Draw the radii from the center O to the points of tangency:
- OP is perpendicular to AB
- OQ is perpendicular to BC
- OR is perpendicular to CD
- OS is perpendicular to DA
We need to show that the angles subtended by the opposite sides at the center O are supplementary. Specifically, we will show that:
∠BOC+∠AOD=180∘
From the properties of tangents, we know that:
- AP=AS (tangents from point A)
- BP=BQ (tangents from point B)
- CQ=CR (tangents from point C)
- DR=DS (tangents from point D)
Using the tangent properties, we can express the angles at the center:
- ∠AOB=∠APB+∠BQA
- ∠COD=∠CRD+∠DSA
The sum of angles around point O in quadrilateral ABCD is:
∠AOB+∠BOC+∠COD+∠DOA=360∘
Since opposite angles are equal, we can simplify:
∠AOB+∠COD=180∘
This implies:
∠BOC+∠AOD=180∘
Thus, we have shown that the opposite sides of the quadrilateral ABCD subtend supplementary angles at the center O.
Similar Questions
Knowledge Check
Find the perimeter of the quadrilateral that circumscribes this circle.
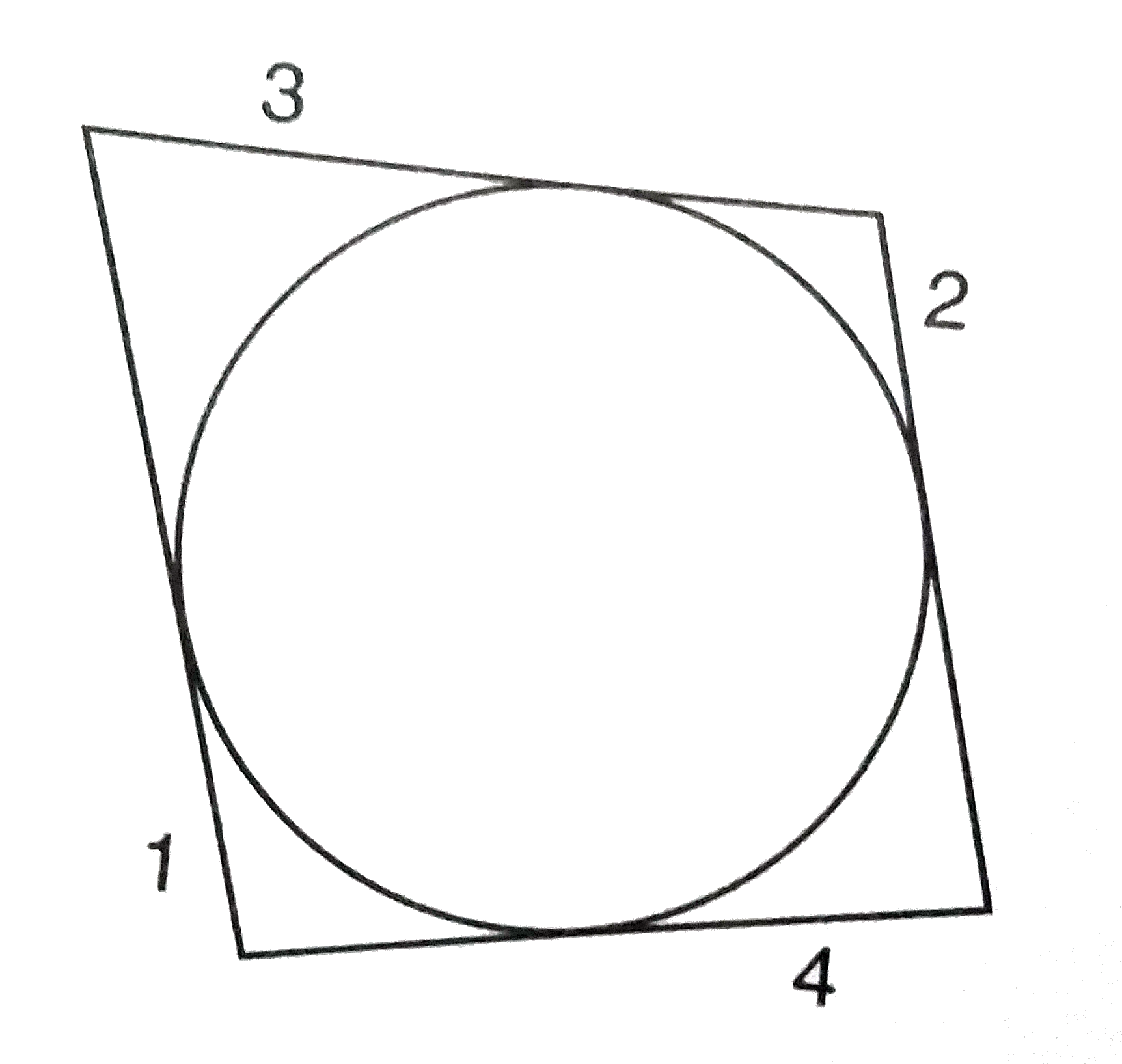 A10B12C15D20
A10B12C15D20
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4 cm, 5cm, and 7cm respectively. Determine the length of the fourth side.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionProve that equal chords of congruent circles subtend equal angles at their centre.
View SolutionProve that the rectangle circumscribing a circle is a square
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View Solution