On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
area of handkerchief =42⋅42=1764cm2
area of 1 circle =πr2=227⋅7⋅7
=154cm2
area of 9 circles is =9⋅154=1386cm2
remaining area =1764−1386
=378cm2
answer
Similar Questions
On a square handkerchief, nine circular designs each of radius 7 cm are made (see Figure). Find the area of the remaining portion of the handkerchief.
View SolutionFrom each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View SolutionFrom each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
View SolutionFrom a rectangular cardboard sheet 145 cm long and 32 cm broad ,42 circular plates each of diameter 8 cm have been cut out . Find the area of the remaining portion of the sheet.
View SolutionA square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 15.37. Find the area of the remaining part of the park (Use π=22/7) . (FIGURE)
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionIn Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
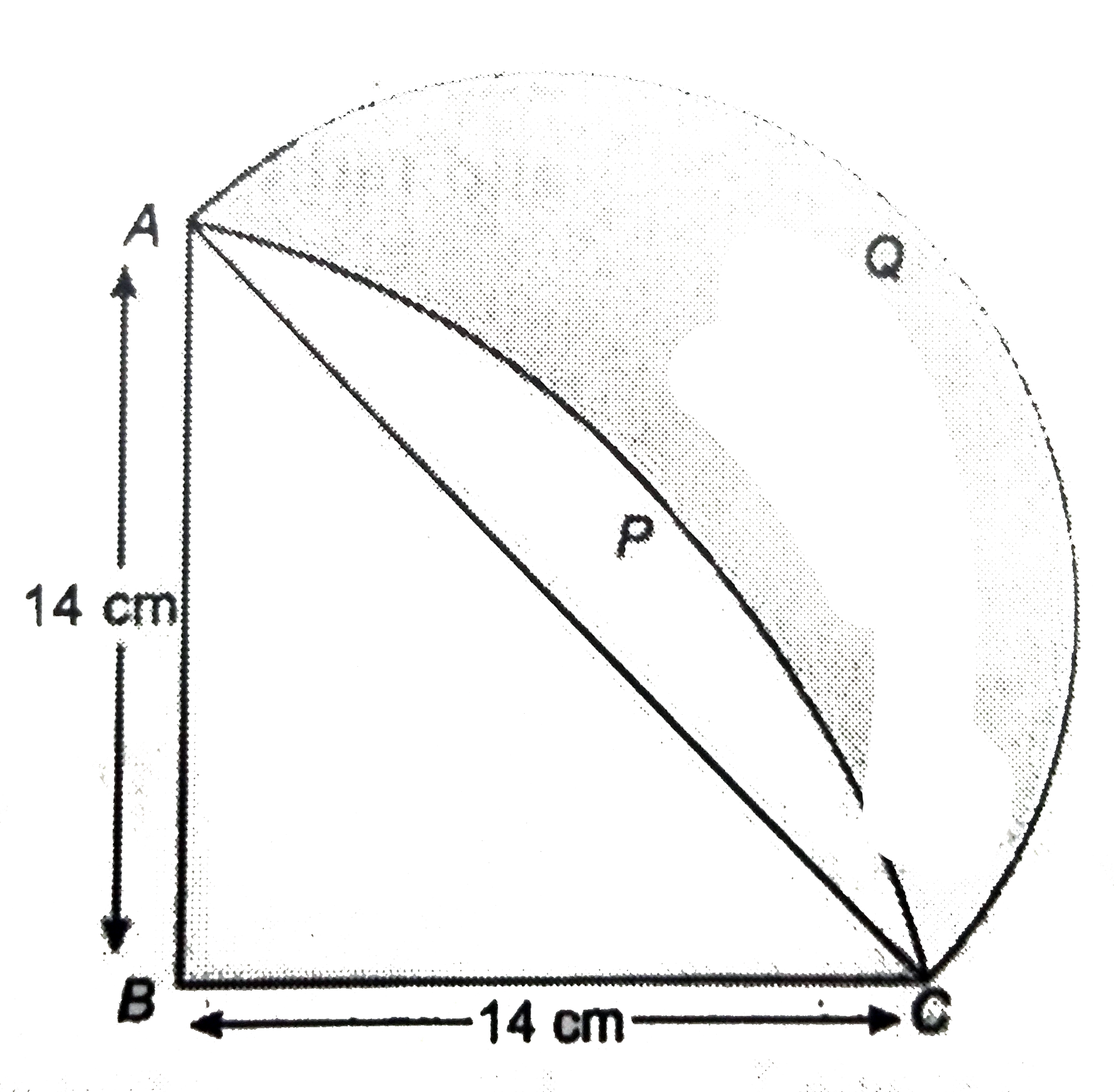
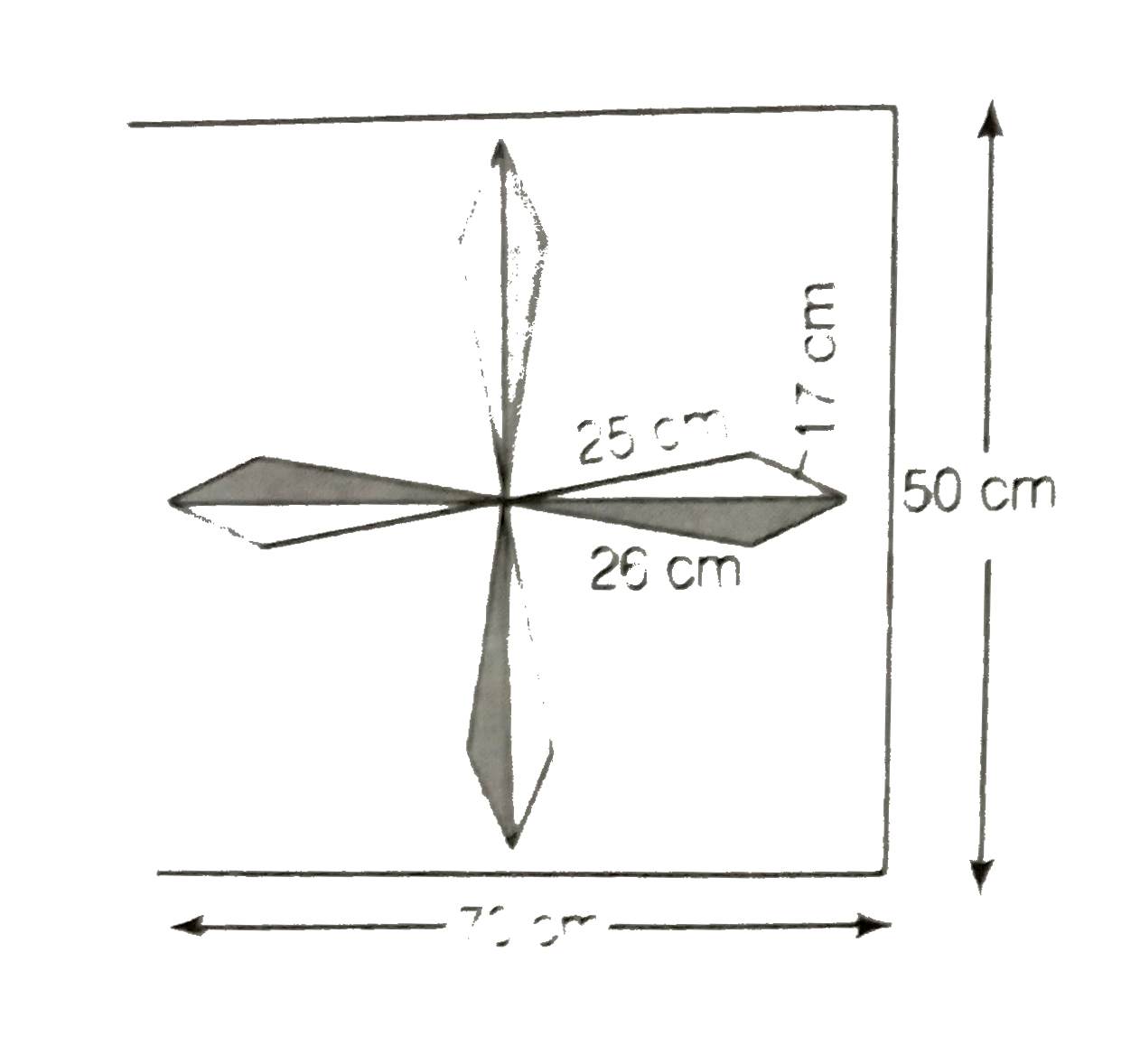
View SolutionA design is made on a rectangular tile of dimensions 50 cm×70 cm as shown in figure. The design shows 8 triangle, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tiles.
View SolutionFrom a circular piece of cardboard of radius 3 cm two sectors of 90∘ have been cut off. Find the perimeter of the remaining portion nearest hundredth centimeters (Take π=227).
View Solution
