Question

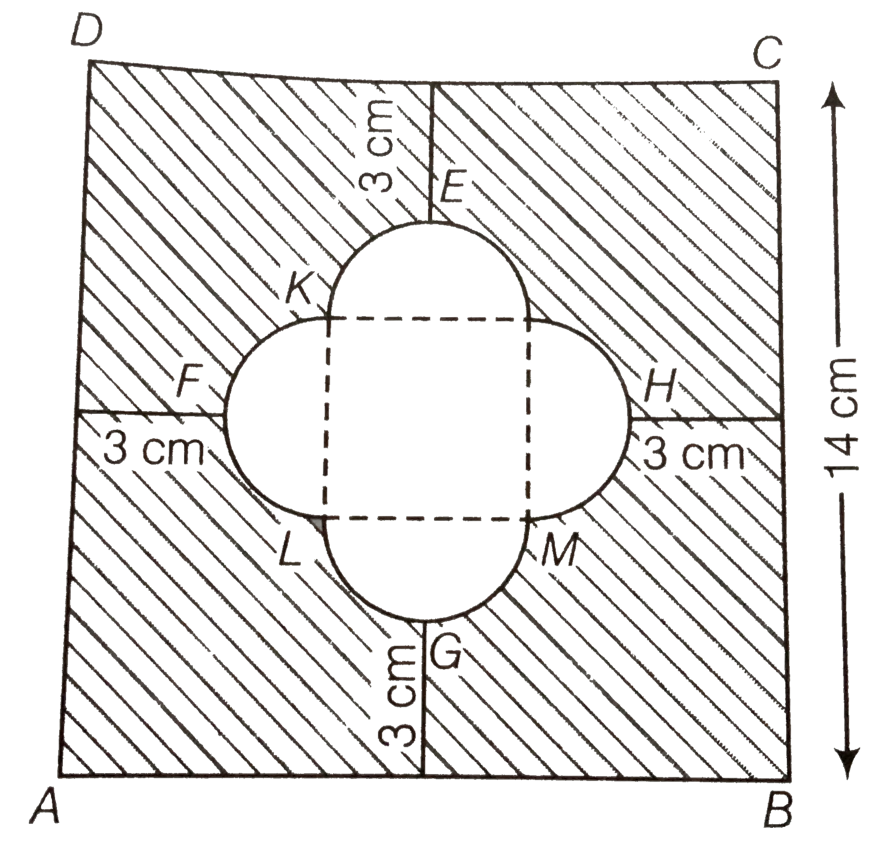
Find the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.

Explanation

To find the area of the shaded region in the given figure where ABCD is a square of side 14 cm, we can follow these steps:

1. Identify the Side of the Square:
The side of the square ABCD is given as 14 cm.

2. Calculate the Area of the Square:
The area of a square is calculated using the formula:
\( \text{Area of square} = \text{side}^2 \)
Substituting the value:
\( \text{Area of square} = 14^2 = 196 \text{ cm}^2 \)

3. Determine the Radius of the Circles:
The figure shows four circles inscribed in the corners of the square. The relationship between the side of the square and the radius \( r \) of the circles is:
\( \text{Side of square} = 4r \)
Therefore, we can find \( r \):
\( 4r = 14 \implies r = \frac{14}{4} = \frac{7}{2} \text{ cm} \)

4. Calculate the Area of One Circle:
The area of a circle is calculated using the formula:
\( \text{Area of circle} = \pi r^2 \)
Substituting the value of \( r \):
\( \text{Area of one circle} = \pi \left(\frac{7}{2}\right)^2 = \pi \cdot \frac{49}{4} = \frac{49\pi}{4} \text{ cm}^2 \)

5. Calculate the Area of Four Circles:
Since there are four circles, the total area of the circles is:
\( \text{Area of four circles} = 4 \times \frac{49\pi}{4} = 49\pi \text{ cm}^2 \)

6. Calculate the Area of the Shaded Region:
The area of the shaded region is found by subtracting the area of the four circles from the area of the square:
\( \text{Area of shaded region} = \text{Area of square} - \text{Area of four circles} \)
Substituting the values:
\( \text{Area of shaded region} = 196 - 49\pi \)

7. Approximate the Value (if needed):
If we use \( \pi \approx \frac{22}{7} \):
\( 49\pi \approx 49 \times \frac{22}{7} = \frac{1078}{7} \approx 154 \text{ cm}^2 \)
Thus, the area of the shaded region becomes:
\( \text{Area of shaded region} \approx 196 - 154 = 42 \text{ cm}^2 \)

Final Answer:
The area of the shaded region is approximately \( 42 \text{ cm}^2 \).