By counting squares, estimate the area of the figure 10.9 b.
To estimate the area of the given figure by counting squares, we will follow these steps:
1. Identify Full Squares: Count the number of full squares in the figure. Each full square contributes an area of 1.
- Count: Let's say we find 11 full squares.
2. Identify Half-Filled Squares: Count the number of squares that are half-filled. Each half-filled square contributes an area of 1/2.
- Count: Let's say we find 3 half-filled squares.
3. Identify More Than Half-Filled Squares: Count the number of squares that are more than half-filled. Each of these squares contributes an area of 1.
- Count: Let's say we find 8 squares that are more than half-filled.
4. Identify Less Than Half-Filled Squares: Count the number of squares that are less than half-filled. These squares do not contribute to the area (considered as 0).
- Count: Let's say we find 5 squares that are less than half-filled.
5. Calculate Total Area: Use the counts from the previous steps to calculate the total area.
- Total Area = (Number of Full Squares) + (Number of Half-Filled Squares × 1/2) + (Number of More Than Half-Filled Squares) + (Number of Less Than Half-Filled Squares × 0)
- Plugging in the values:
Total Area=11+(3×12)+8+(5×0)
=11+32+8+0
6. Convert to a Common Denominator: To add these, convert to a common denominator (which is 2):
- Convert 11 to a fraction: 11=222
- Convert 8 to a fraction: 8=162
- Now add them:
=222+32+162
=22+3+162=412
7. Convert to Mixed Number (if needed): If you want to express this as a mixed number:
- 412=2012
Final Answer:
The estimated area of the figure is 412 or 2012.
---
- Count: Let's say we find 11 full squares.
- Count: Let's say we find 3 half-filled squares.
- Count: Let's say we find 8 squares that are more than half-filled.
- Count: Let's say we find 5 squares that are less than half-filled.
- Total Area = (Number of Full Squares) + (Number of Half-Filled Squares × 1/2) + (Number of More Than Half-Filled Squares) + (Number of Less Than Half-Filled Squares × 0)
- Plugging in the values:
Total Area=11+(3×12)+8+(5×0)
=11+32+8+0
- Convert 11 to a fraction: 11=222
- Convert 8 to a fraction: 8=162
- Now add them:
=222+32+162
=22+3+162=412
- 412=2012
The estimated area of the figure is 412 or 2012.
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.2
1 Videos
- MENSURATIONBOOK - NCERT ENGLISHCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.1
16 Videos
- KNOWING OUR NUMBERSBOOK - NCERT ENGLISHCHAPTER - KNOWING OUR NUMBERSEXERCISE - EXERCISE 1.3
3 Videos
- PLAYING WITH NUMBERSBOOK - NCERT ENGLISHCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.1
4 Videos
Similar Questions
Knowledge Check
The 8-sided figure below is divided into 5 congruent squares. The total area of the 5 squares is 125 square inches. What is the perimeter, in inches, of the figure?
 A25B60C80D100
A25B60C80D100The area of a square is 1 sq. m Express the area of this square is sq. mm.
A1,00,00,000 sq mmB10,00,000 sq mmC1,00,000 sq mmD20,00,000 sq mm
Draw any circle on the graph paper. Count the squares and use them to estimate the area of the circular region.
View SolutionFind the area of the shape shown in the figure 10.10.
View Solution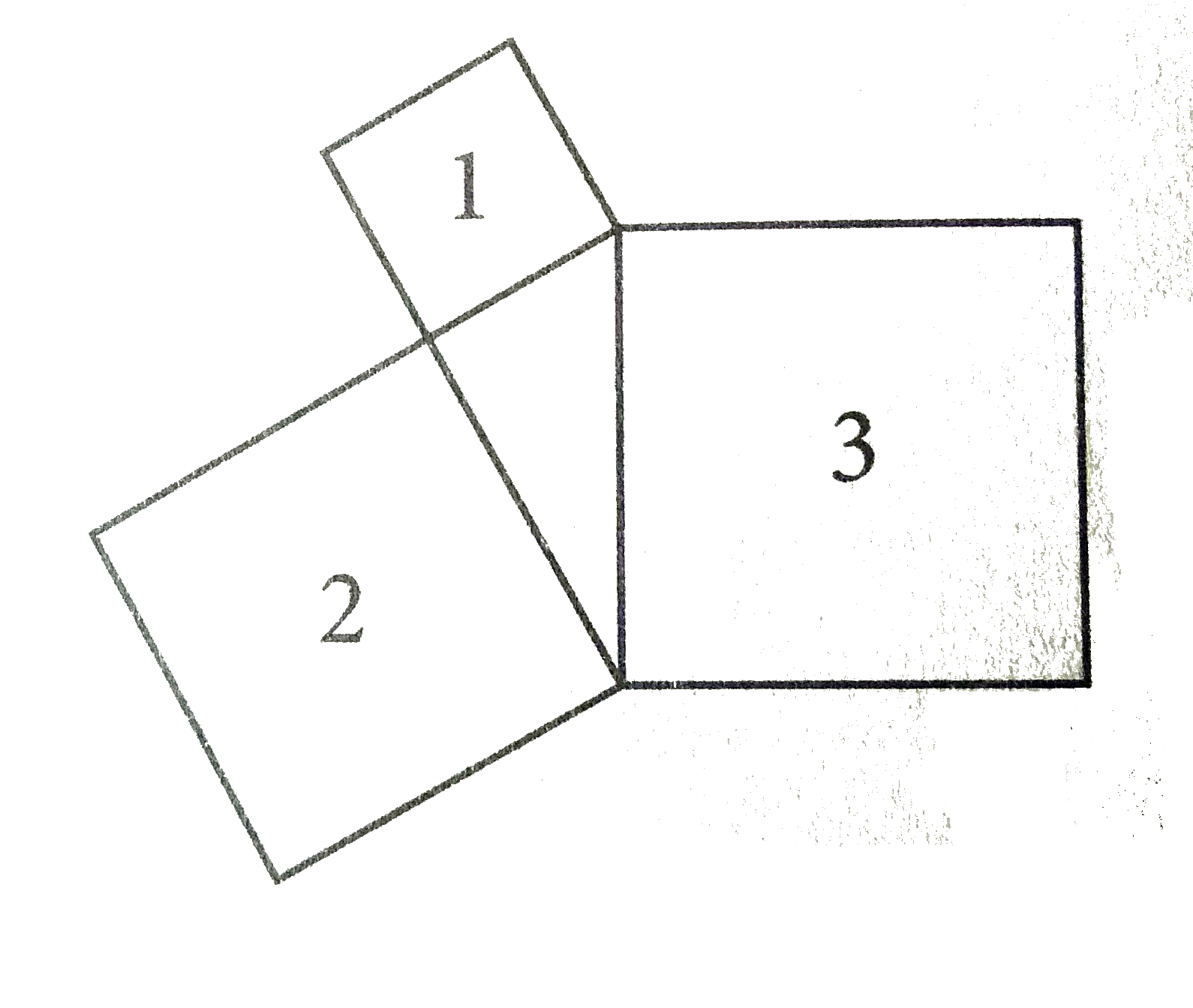
Each of the quadrilaterals figure above is a square. The area of the smallest square (square 1) is 16 square units, and the area of the medium square (square 2) is 48 square units. What is the area, in square units, of the largest square (square 3)?
View Solution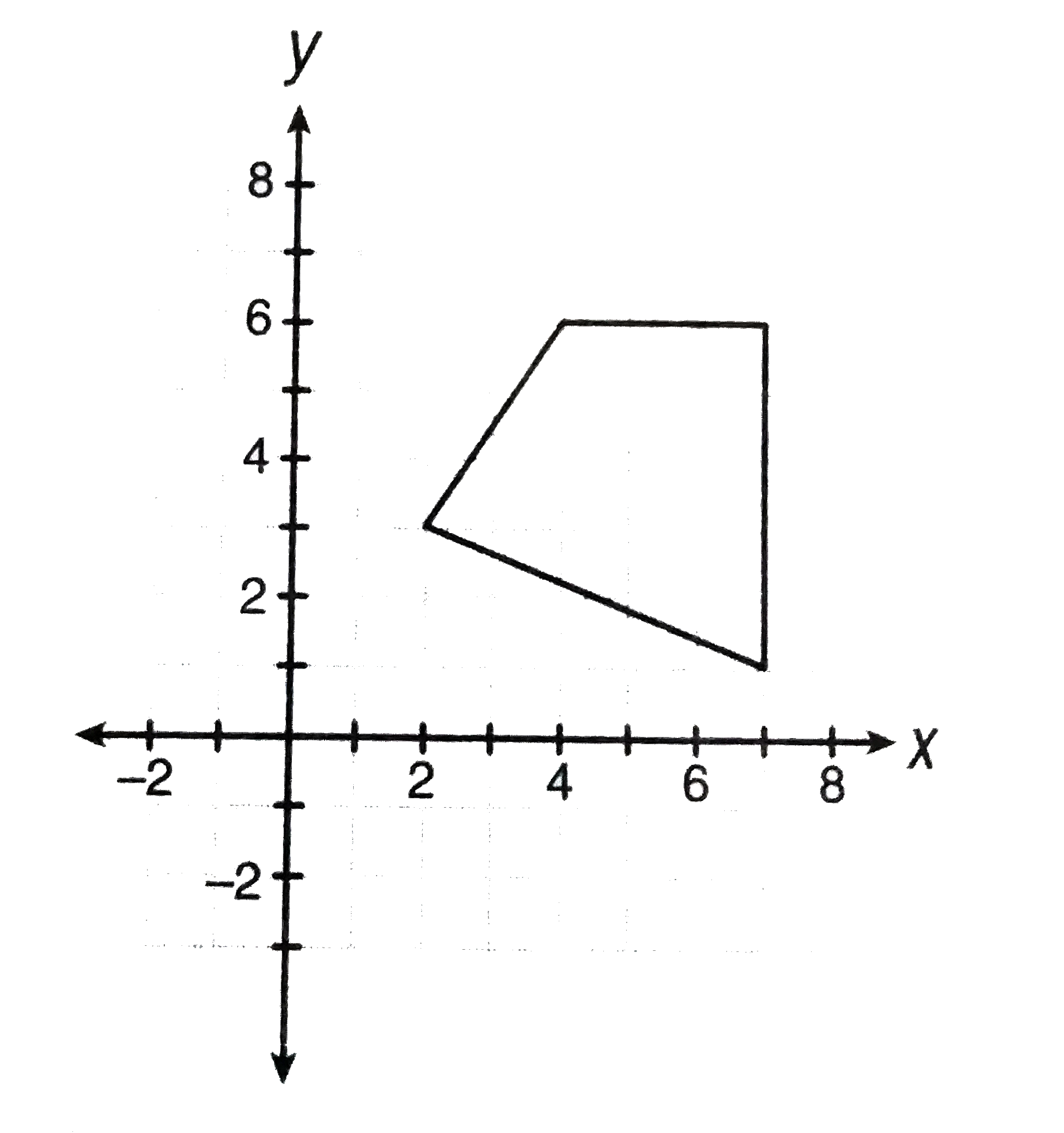
what is the number of square units in the area of the quandrilateral shown in the figure above?
View SolutionIn the adjoining figure, ABCD is a square of side 10 cm and two semicircles with side of the square as diameter. A quarter circle is also seen in figure with side of square as radius. Find the area of the square region excluding the shaded part . (Take π=3.14)

View SolutionIn Figure ABCD is a square with side 7 cm. A circle is drawn circumscribing the square . Find the area of the shaded region .

View Solution

